题目内容
6.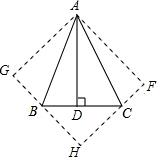 如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.
如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.(1)求证:四边形AFHG为正方形;
(2)若BD=6,CD=4,求AB的长.
分析 (1)由折叠的性质可得到的条件是:①AG=AD=AF,②∠GAF=∠GAD+∠DAF=2∠BAC=90°,且∠G=∠F=90°;由②可判定四边形AGHF是矩形,由AG=AF可证得四边形AGHF是正方形;
(2)设AD=x,由折叠的性质可得:AD=AF=x(即正方形的边长为x),BG=BD=6,CF=CD=4;进而可用x表示出BH、HC的长,即可在Rt△BHC中,由勾股定理求得AD的长,进而可求出AB的长.
解答 证明:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°;
由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,
∠BAG=∠BAD,∠CAF=∠CAD,
∴∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°;
∴∠GAF=∠BAG+∠CAF+∠BAC=90°;
∴四边形AFHG是正方形,
解:(2)∵四边形AFHG是正方形,
∴∠BHC=90°,
又GH=HF=AD,GB=BD=6,CF=CD=4;
设AD的长为x,则BH=GH-GB=x-6,CH=HF-CF=x-4.
在Rt△BCH中,BH2+CH2=BC2,
∴(x-6)2+(x-4)2=102,
解得x1=12,x2=-2(不合题意,舍去),
∴AD=12,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{144+36}$=6$\sqrt{5}$.
点评 此题主要考查了垂径定理、勾股定理、正方形的判定和性质以及图形的翻折变换等知识,能够根据折叠的性质得到与所求相关的相等角和相等边是解答此题的关键.

练习册系列答案
相关题目
15.长沙红星大市场某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获利润500元,其利润率为20%.现如果按同一标价打九折销售该电器一件,那么获得的纯利润为( )
| A. | 562.5元 | B. | 875元 | C. | 550元 | D. | 750元 |
 如图,把一张对边平行的长方形ABCD(AD∥BC,AB∥DC)的纸片沿EF折叠后,ED、BC的交点为G,点D、C分别落在D′C′的位置上,若∠EFG=55°,求∠EGF的度数.
如图,把一张对边平行的长方形ABCD(AD∥BC,AB∥DC)的纸片沿EF折叠后,ED、BC的交点为G,点D、C分别落在D′C′的位置上,若∠EFG=55°,求∠EGF的度数.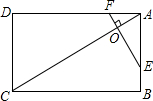 如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.
如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.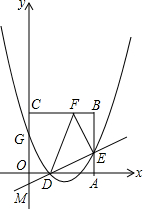 如图所示,正方形OABC的边长为2cm,以OA、OC所在直线为坐标轴建立直角坐标系xoy,点D、E、F和G分别从点O、A、B和C沿着OA、AB、BC和CO方向都以1cm/s的速度同时移动,移动时间为t(0<t<2)s,抛物线y=ax2+bx+c总是经过三个动点G、D、E.
如图所示,正方形OABC的边长为2cm,以OA、OC所在直线为坐标轴建立直角坐标系xoy,点D、E、F和G分别从点O、A、B和C沿着OA、AB、BC和CO方向都以1cm/s的速度同时移动,移动时间为t(0<t<2)s,抛物线y=ax2+bx+c总是经过三个动点G、D、E.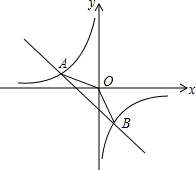 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,n).
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,n).