题目内容
18.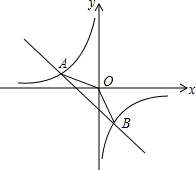 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,n).
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,n).(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
分析 (1)将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例函数解析式;将B坐标代入反比例解析式中求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出a与b的值,即可确定出一次函数解析式;
(2)设直线AB与y轴交于点C,求得点C坐标,S△AOB=S△AOC+S△COB,计算即可;
(3)由图象直接可得自变量x的取值范围.
解答 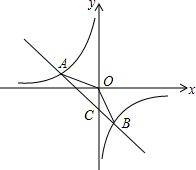 解:(1)∵A(-2,1),
解:(1)∵A(-2,1),
∴将A坐标代入反比例函数解析式y2=$\frac{m}{x}$中,得m=-2,
∴反比例函数解析式为y=-$\frac{2}{x}$;
将B坐标代入y=-$\frac{2}{x}$,得n=-2,
∴B坐标(1,-2),
将A与B坐标代入一次函数解析式中,得$\left\{\begin{array}{l}{-2a+b=1}\\{a+b=-2}\end{array}\right.$,
解得a=-1,b=-1,
∴一次函数解析式为y1=-x-1;
(2)设直线AB与y轴交于点C,
令x=0,得y=-1,
∴点C坐标(0,-1),
∴S△AOB=S△AOC+S△COB=$\frac{1}{2}$×1×2+$\frac{1}{2}$×1×1=$\frac{3}{2}$;
(3)由图象可得,当y1<y2<0时,自变量x的取值范围x>1.
点评 本题属于反比例函数与一次函数的交点问题,涉及的知识有:待定系数法求函数解析式,三角形面积的求法,坐标与图形性质,利用了数形结合的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
8.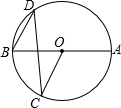 如图,AB是⊙O的直径,C,D为圆上两点,若∠AOC=130°,则∠D等于( )
如图,AB是⊙O的直径,C,D为圆上两点,若∠AOC=130°,则∠D等于( )
 如图,AB是⊙O的直径,C,D为圆上两点,若∠AOC=130°,则∠D等于( )
如图,AB是⊙O的直径,C,D为圆上两点,若∠AOC=130°,则∠D等于( )| A. | 20° | B. | 25° | C. | 35° | D. | 50° |
3. 如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )
如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )
 如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )
如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )| A. | $\frac{13}{3}$ | B. | $\frac{9}{2}$ | C. | $\frac{4}{3}$$\sqrt{13}$ | D. | 2$\sqrt{5}$ |
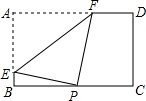 如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是6-2$\sqrt{5}$≤x≤4.
如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是6-2$\sqrt{5}$≤x≤4.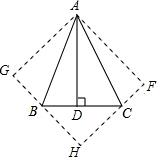 如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.
如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.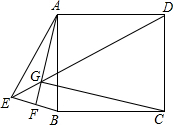 已知E是正方形ABCD外一点,且AB=AE,连BE作AF⊥BE,垂足为F,连DE交AF于G.
已知E是正方形ABCD外一点,且AB=AE,连BE作AF⊥BE,垂足为F,连DE交AF于G.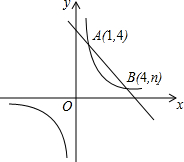 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.