题目内容
1.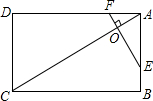 如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.
如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.(1)求证:△AEF∽△BCA;
(2)若$\frac{OA}{OC}$=$\frac{1}{4}$,BC=2AB,求$\frac{AF}{DF}$.
分析 (1)由矩形的性质得出∠B=∠BAD=90°,再证出∠AEF=∠BCA,即可证出△AEF∽△BCA;
(2)先证出△AOF∽△EAF,得出△AOF∽△CBA,得出对应边成比例$\frac{AF}{AC}=\frac{OA}{BC}$,设OA=x,则AC=5x,由BC=2AB,得出AD=2$\sqrt{5}$x,求出AF,得出DF,即可求出$\frac{AF}{DF}$.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,AD=BC,
∴∠CAB+∠BCA=90°,
∵EF⊥AC,
∴∠AOE=∠AOF=90°,
∴∠CAB+∠AEF=90°,
∴∠AEF=∠BCA,
∴△AEF∽△BCA;
(2)解:∵∠AFO=∠EFA,∠AOF=∠EAF=90°,
∴△AOF∽△EAF,
∴△AOF∽△CBA,
∴$\frac{AF}{AC}=\frac{OA}{BC}$,
∵$\frac{OA}{OC}$=$\frac{1}{4}$,
∴AC=5OA,
设OA=x,则AC=5x,
∵BC=2AB,
∴AB=$\sqrt{5}$x,AD=BC=2$\sqrt{5}$x,
∴$\frac{AF}{5x}=\frac{x}{2\sqrt{5}x}$,
∴AF=$\frac{\sqrt{5}x}{2}$,
∴DF=2$\sqrt{5}$x-$\frac{\sqrt{5}x}{2}$=$\frac{3\sqrt{5}x}{2}$,
∴$\frac{AF}{DF}$=$\frac{1}{3}$.
点评 本题考查了矩形的性质、相似三角形的判定与性质、勾股定理;熟练掌握矩形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
11.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
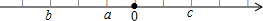 如图,a,b,c在数轴上的位置,求代数式$\sqrt{{a}^{2}}$-|a-b|+$\sqrt{{a}^{2}-2ac+{c}^{2}}$.
如图,a,b,c在数轴上的位置,求代数式$\sqrt{{a}^{2}}$-|a-b|+$\sqrt{{a}^{2}-2ac+{c}^{2}}$.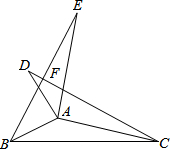 如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=150°,则∠EFC的度数为60°.
如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=150°,则∠EFC的度数为60°.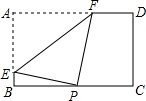 如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是6-2$\sqrt{5}$≤x≤4.
如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是6-2$\sqrt{5}$≤x≤4.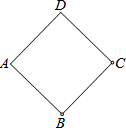 如图,正方形ABCD,边长AB=2.
如图,正方形ABCD,边长AB=2.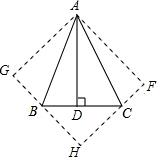 如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.
如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.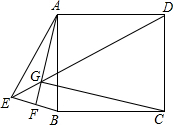 已知E是正方形ABCD外一点,且AB=AE,连BE作AF⊥BE,垂足为F,连DE交AF于G.
已知E是正方形ABCD外一点,且AB=AE,连BE作AF⊥BE,垂足为F,连DE交AF于G.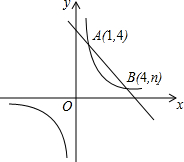 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.