题目内容
14．
如图，把一张对边平行的长方形ABCD（AD∥BC，AB∥DC）的纸片沿EF折叠后，ED、BC的交点为G，点D、C分别落在D′C′的位置上，若∠EFG=55°，求∠EGF的度数．
分析 由折叠的性质得出∠GEF=∠DEF，由矩形的性质得出内错角相等∠DEF=∠EFG=55°，同旁内角互补∠EGF+∠DEG=180°，求出∠DEG，即可得出∠EGF．
解答 解：根据题意得：∠GEF=∠DEF，
∵AD∥BC，
∴∠DEF=∠EFG=55°，∠EGF+∠DEG=180°，
∴∠GEF=55°，
∴∠DEG=110°，
∴∠EGF=70°．
点评 本题考查了矩形的性质、折叠的性质、平行线的性质；熟练掌握矩形和折叠的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
4．在一次捐款中，某班第一组有10名同学，其捐款数额统计如下表：
则捐款数额组成的一组数据中，中位数是17.5．
| 捐款（元） | 10 | 15 | 20 | 50 |
| 人数 | 1 | 4 | 3 | 2 |
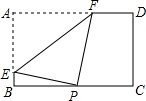如图，矩形纸片ABCD中，AB=4，AD=6，点P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别为E、F，要使折痕始终与边AB、AD有交点，则BP的取值范围是6-2$\sqrt{5}$≤x≤4．
如图所示是一个等腰三角形纸片ABC，其中AB=AC，把∠B沿EM折叠，使点B落在点D上，把∠C沿FN折叠，使点C也落在点D上．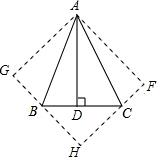
如图，在△ABC中，∠BAC=45°，AD⊥BC于D，将△ACD沿AC折叠为△ACF，将△ABD沿AB折叠为△ABG，延长FC和GB相交于点H．
3．
如图，在矩形ABCD中，AB=4，AD=5，AD，AB，BC分别与⊙O相切于E，F，G三点，过点D作⊙O的切线BC于点M，切点为N，则DM的长为（ ）
如图，在矩形ABCD中，AB=4，AD=5，AD，AB，BC分别与⊙O相切于E，F，G三点，过点D作⊙O的切线BC于点M，切点为N，则DM的长为（ ）| A． | $\frac{13}{3}$ | B． | $\frac{9}{2}$ | C． | $\frac{4}{3}$$\sqrt{13}$ | D． | 2$\sqrt{5}$ |