题目内容
16.若实数a、b满足(4a+4b)(4a+4b-2)-8=0,则a+b=-$\frac{1}{2}$或1.分析 设a+b=x,则原方程转化为关于x的一元二次方程,通过解该一元二次方程来求x即(a+b)的值.
解答 解:设a+b=x,则由原方程,得
4x(4x-2)-8=0,
整理,得16x2-8x-8=0,即2x2-x-1=0,
分解得:(2x+1)(x-1)=0,
解得:x1=-$\frac{1}{2}$,x2=1.
则a+b的值是-$\frac{1}{2}$或1.
故答案是:-$\frac{1}{2}$或1.
点评 本题主要考查了换元法,即把某个式子看作一个整体,用一个字母去代替它,实行等量替换.

练习册系列答案
相关题目
4.观察下列各式及其展开式:
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
…
请你猜想(a+b)10的展开式第三项的系数是( )
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
…
请你猜想(a+b)10的展开式第三项的系数是( )
| A. | 36 | B. | 45 | C. | 55 | D. | 66 |
11.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
5.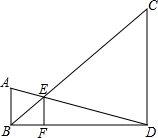 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
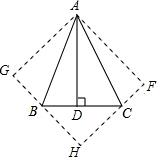 如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.
如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.




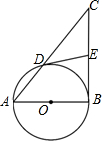 如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE.
如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE.