题目内容
我们知道:1+2=
=3;1+2+3=
=6;1+2+3+4=
=10;则:
1+2+3+4+5= ;(算出结果)
1+2+3+4+…+100= ;
1+2+3+4+…+n= .
| 2×(2+1) |
| 2 |
| 3×(3+1) |
| 2 |
| 4×(4+1) |
| 2 |
1+2+3+4+5=
1+2+3+4+…+100=
1+2+3+4+…+n=
考点:规律型:数字的变化类
专题:
分析:根据观察,可得连续自然数的求和公式:1+2+3+…+n=
,根据求和公式,逐一计算即可得出答案.
| n(n+1) |
| 2 |
解答:解:1+2+3+4+5=
=15;
1+2+3+4+…+100=
=505;
1+2+3+4+…+n=
.
故答案为:15;5050;
.
| 5×(5+1) |
| 2 |
1+2+3+4+…+100=
| 100×(100+1) |
| 2 |
1+2+3+4+…+n=
| n(n+1) |
| 2 |
故答案为:15;5050;
| n(n+1) |
| 2 |
点评:此题考查数字的变化规律,找出数字之间的联系,发现规律,利用规律解决问题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
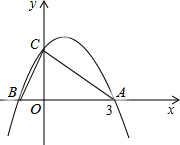 如图,抛物线y=-x2+2x+m与x轴相交于点A(3,0)和B,与y轴相交于点C.
如图,抛物线y=-x2+2x+m与x轴相交于点A(3,0)和B,与y轴相交于点C.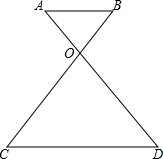 如图,AD与BC交与点O,且AB∥CD.
如图,AD与BC交与点O,且AB∥CD.