题目内容
用因式分解法解下列方程:
(1)y(y+5)=-
(2)3(x-3)=(x-3)2
(3)(2x+3)2=24x
(4)4x2=4
x-5.
(1)y(y+5)=-
| 25 |
| 4 |
(2)3(x-3)=(x-3)2
(3)(2x+3)2=24x
(4)4x2=4
| 5 |
考点:解一元二次方程-因式分解法
专题:
分析:(1)根据因式分解法:完全平方公式,可得方程的解;
(2)根据因式分解法:提公因式分解因式,可得方程的解;
(3)根据因式分解法:完全平方公式,可得方程的解;
(4)根据因式分解法:完全平方公式,可得方程的解.
(2)根据因式分解法:提公因式分解因式,可得方程的解;
(3)根据因式分解法:完全平方公式,可得方程的解;
(4)根据因式分解法:完全平方公式,可得方程的解.
解答:解:(1)将方程化为一般式,得
y2+5y+
=0,
因式分解,得
(y+
)2=0,
解得y1=y2=-
;
(2)移项得3(x-3)-(x-3)2=0,
因式分解,得
(x-3)[3-(x-3)]=0
即x-3=0或6-x=0,
解得x1=3,x2=6;
(3)将方程化为一般式,得
4x2-12x+9=0,
因式分解,得(2x-3)2=0,
解得x1=x2=
;
(4)将方程化为一般式,得
4x2-4
x+5=0,
因式分解,得
(2x-
)2=0,
解得x1=x2=
.
y2+5y+
| 25 |
| 4 |
因式分解,得
(y+
| 5 |
| 2 |
解得y1=y2=-
| 5 |
| 2 |
(2)移项得3(x-3)-(x-3)2=0,
因式分解,得
(x-3)[3-(x-3)]=0
即x-3=0或6-x=0,
解得x1=3,x2=6;
(3)将方程化为一般式,得
4x2-12x+9=0,
因式分解,得(2x-3)2=0,
解得x1=x2=
| 3 |
| 2 |
(4)将方程化为一般式,得
4x2-4
| 5 |
因式分解,得
(2x-
| 5 |
解得x1=x2=
| ||
| 2 |
点评:本题考查了解一元二次方程,利用了提公因式分解因式,完全平方公式分解因式.

练习册系列答案
相关题目
某洗衣机经过连续两次降价,每台售价由原来的1500元降到了990元.设平均每次降价的百分率为x,则下列方程中正确的是( )
| A、1500(1+x)2=990 |
| B、990(1+x)2=1500 |
| C、1500(1-x)2=990 |
| D、990(1-x)2=1500 |
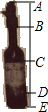 如图所示,的是一种盛装葡萄酒的瓶子,分为瓶塞AB,瓶颈BC,标签CD和瓶底DE四部分,已知;AB:BC=2;3,且DE=
如图所示,的是一种盛装葡萄酒的瓶子,分为瓶塞AB,瓶颈BC,标签CD和瓶底DE四部分,已知;AB:BC=2;3,且DE= 如图,在?ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.求证:
如图,在?ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.求证: 如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积为
如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积为