题目内容
小明销售一种文具.销售过程中发现,如果将进价为8元/件的文具按每件10元出售,每天可销售100件.现采用提高售价,减少进货量的办法增加利润,已知这种商品的销售单价每增加1元,其日销售量就要减少10件.设销售价为x元/件时,日销量为y个.
(1)求y关于x的函数关系式;
(2)当销售单价定为多少元时,每日可获得最大利润?最大利润为多少?
(1)求y关于x的函数关系式;
(2)当销售单价定为多少元时,每日可获得最大利润?最大利润为多少?
考点:二次函数的应用
专题:
分析:(1)设售价定为每件x元,根据日销量=原来销量-减少销量,列函数关系式即可;
(2)设每天的利润为y元,根据总利润=每件利润×销售数量建立函数关系式,再由函数的性质进一步分析解答即可.
(2)设每天的利润为y元,根据总利润=每件利润×销售数量建立函数关系式,再由函数的性质进一步分析解答即可.
解答:解:(1)设定价为x元,由题意得
y=100-10(x-10)=200-10x;
(2)设每天的利润为y元,由题意得
y=(x-8)[100-10(x-10)]=-10(x-14)2+360,
∵-10<0.
∴当定价为14元时有最大利润为360元.
y=100-10(x-10)=200-10x;
(2)设每天的利润为y元,由题意得
y=(x-8)[100-10(x-10)]=-10(x-14)2+360,
∵-10<0.
∴当定价为14元时有最大利润为360元.
点评:此题考查了一元二次方程和二次函数的运用,利用总利润=单个利润×销售数量建立函数关系式,进一步利用性质的解决问题,解答时求出二次函数的解析式是关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
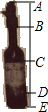 如图所示,的是一种盛装葡萄酒的瓶子,分为瓶塞AB,瓶颈BC,标签CD和瓶底DE四部分,已知;AB:BC=2;3,且DE=
如图所示,的是一种盛装葡萄酒的瓶子,分为瓶塞AB,瓶颈BC,标签CD和瓶底DE四部分,已知;AB:BC=2;3,且DE=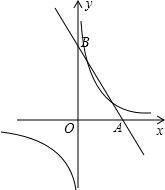 已知,如图,函数y=
已知,如图,函数y=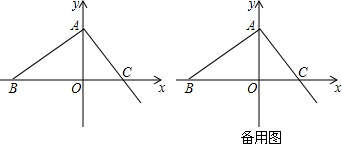
 如图,DE∥BC,DF∥AB,∠1=70°,求∠D、∠2和∠3的度数.
如图,DE∥BC,DF∥AB,∠1=70°,求∠D、∠2和∠3的度数.