题目内容
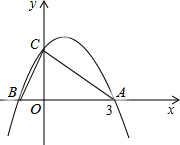 如图,抛物线y=-x2+2x+m与x轴相交于点A(3,0)和B,与y轴相交于点C.
如图,抛物线y=-x2+2x+m与x轴相交于点A(3,0)和B,与y轴相交于点C.(1)求m的值和点B的坐标;
(2)点D(x,y)是抛物线上一点,若S△ABD=S△ABC,求点D的坐标.
考点:抛物线与x轴的交点
专题:
分析:(1)把点A的坐标代入函数解析式,通过解方程来求m的值;利用抛物线的对称性来求点B的坐标;
(2)由(1)可知设D的坐标为(x,-x2+2x+3),由已知条件易求S△ABC,并且△ABD的高为D的纵坐标的绝对值,所以可建立方程求出x的值即可.
(2)由(1)可知设D的坐标为(x,-x2+2x+3),由已知条件易求S△ABC,并且△ABD的高为D的纵坐标的绝对值,所以可建立方程求出x的值即可.
解答:解:(1)∵抛物线y=-x2+2x+m与x轴相交于点A(3,0),
∴-32+2×3+m=0,
解得 m=3.
∵该抛物线的对称轴为:x=1,
∴B(-1,0);
(2)由(1)可知设D的坐标为(x,-x2+2x+3),
∵AB=4,OC=3,
∴S△ABC=
×4×3=6,
∵S△ABD=S△ABC,
∴
•AB•|-x2+2x+3|=6,
∴D的坐标是(1±
,±3).
∴-32+2×3+m=0,
解得 m=3.
∵该抛物线的对称轴为:x=1,
∴B(-1,0);
(2)由(1)可知设D的坐标为(x,-x2+2x+3),
∵AB=4,OC=3,
∴S△ABC=
| 1 |
| 2 |
∵S△ABD=S△ABC,
∴
| 1 |
| 2 |
∴D的坐标是(1±
| 7 |
点评:此题考查了抛物线与x轴的交点,涉及了待定系数法求函数解析式、一元二次方程的解及三角形的面积,综合性较强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
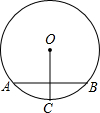 如图,⊙O的一条弦AB垂直平分半径OC,且AB=2
如图,⊙O的一条弦AB垂直平分半径OC,且AB=2| 3 |
| A、6 | ||
B、6
| ||
| C、12 | ||
D、12
|
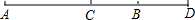 如图,C为线段AD上一点,点B为CD的中点,且AD=12cm,AC=4BC.
如图,C为线段AD上一点,点B为CD的中点,且AD=12cm,AC=4BC.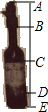 如图所示,的是一种盛装葡萄酒的瓶子,分为瓶塞AB,瓶颈BC,标签CD和瓶底DE四部分,已知;AB:BC=2;3,且DE=
如图所示,的是一种盛装葡萄酒的瓶子,分为瓶塞AB,瓶颈BC,标签CD和瓶底DE四部分,已知;AB:BC=2;3,且DE=