题目内容
某小商场以每件20元的价格购进一种服装,先试销一周,当售价为38元/件时,每天销量为4件,以后每降价2元/件,则销量增加4件,设销量为t(件),每件的销售价为x(元/件)
(1)试求t与x之间的函数关系式;
(2)在商品不积压且不考虑其它因素的条件下,每件服装的销售定价为多少时,该小商场销售这种服装每天获得的毛利润最大?每天的最大毛利润是多少?(注:每件服装销售的毛利润=每件服装的销售价-每件服装的进货价)
(1)试求t与x之间的函数关系式;
(2)在商品不积压且不考虑其它因素的条件下,每件服装的销售定价为多少时,该小商场销售这种服装每天获得的毛利润最大?每天的最大毛利润是多少?(注:每件服装销售的毛利润=每件服装的销售价-每件服装的进货价)
考点:二次函数的应用
专题:
分析:(1)设y与x的函数关系式为t=kx+b,将x=38,y=4;x=36,y=8分别代入求出k、b,即可得到k与x之间的函数关系式;
(2)根据利润=(售价-成本)×销售量列出函数关系式,利用二次函数的性质即可求出小商场销售这种服装每天获得的毛利润最大值以及每天的最大毛利润是多少.
(2)根据利润=(售价-成本)×销售量列出函数关系式,利用二次函数的性质即可求出小商场销售这种服装每天获得的毛利润最大值以及每天的最大毛利润是多少.
解答:解:(1)设t与x之间的函数关系式为:t=kx+b,因为函数的图象经过(38,4)和(36,8)两点,
∴
,
解得:
.
故t=-2x+80.
(2)设每天的毛利润为w元,每件服装销售的毛利润为(x-20)元,每天售出(80-2x)件,
则w=(x-20)(80-2x)=-2x2+120x-1600=-2(x-30)2+200,
当x=30时,获得的毛利润最大,最大毛利润为200元.
∴
|
解得:
|
故t=-2x+80.
(2)设每天的毛利润为w元,每件服装销售的毛利润为(x-20)元,每天售出(80-2x)件,
则w=(x-20)(80-2x)=-2x2+120x-1600=-2(x-30)2+200,
当x=30时,获得的毛利润最大,最大毛利润为200元.
点评:本题主要考查运用待定系数法求一次函数的解析式及二次函数的应用,根据利润=(售价-成本)×销售量列出函数关系式,另外要熟练掌握二次函数求最值的方法.

练习册系列答案
相关题目
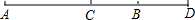 如图,C为线段AD上一点,点B为CD的中点,且AD=12cm,AC=4BC.
如图,C为线段AD上一点,点B为CD的中点,且AD=12cm,AC=4BC.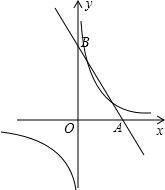 已知,如图,函数y=
已知,如图,函数y=
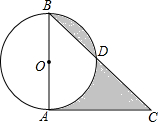 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则阴影部分的面积为
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则阴影部分的面积为