题目内容
17.如图①,在6×6的正方形网格中,每个小正方形的边长均为1,每个小正方形顶点叫做格点.△ABC的顶点在格点上,在图②、图③两个网格中画出一个与△ABC相似的三角形.要求:所画的三角形的顶点在格点上,相似比各不相同且与△ABC的相似比不为1.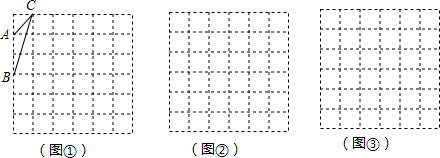
分析 利用相似三角形的性质将各边扩大2倍或使对应边的比为:$\sqrt{2}$:$\sqrt{5}$扩大得出答案即可.
解答  解:如图所示:
解:如图所示:
点评 此题主要考查了相似变换,根据题意正确利用相似三角形的性质得出对应边的长是解题关键.

练习册系列答案
相关题目
5. 实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
 实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )| A. | x+y+z>0 | B. | x+y+z<0 | C. | xy<yz | D. | xy<xz |
2.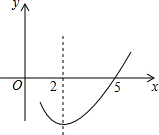 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )
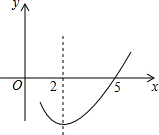 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )| A. | 当x>2时,y随x增大而减小 | B. | 4a=b | ||
| C. | 图象过点(-1,0) | D. | 9a+3b+c>0 |
9. 如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )
如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )
 如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )
如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{9}$ |
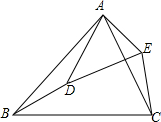 已知:如图,在△ABC和△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.
已知:如图,在△ABC和△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.


