题目内容
12.直线y=-2x+m与直线y=2x-1的交点在第四象限,则m的取值范围在数轴上表示正确的是( )| A. |  | B. |  | ||
| C. |  | D. |  |
分析 利用两直线相交的问题,通过解方程组$\left\{\begin{array}{l}{y=-2x+m}\\{y=2x-1}\end{array}\right.$得两直线的交点坐标为($\frac{m+1}{4}$,$\frac{m-1}{2}$),再利用第四象限点的坐标特征得到$\frac{m+1}{4}$>0且$\frac{m-1}{2}$<0,解得-1<m<1,然后用数轴表示出m的范围.
解答 解:解方程组$\left\{\begin{array}{l}{y=-2x+m}\\{y=2x-1}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{m+•1}{4}}\\{y=\frac{m-1}{2}}\end{array}\right.$,
所以两直线的交点坐标为($\frac{m+1}{4}$,$\frac{m-1}{2}$),
根据题意得$\frac{m+1}{4}$>0且$\frac{m-1}{2}$<0,解得-1<m<1,
用数轴表示为: .
.
故选C.
点评 本题考查了在数轴上表示不等式的解集:用数轴表示不等式的解集时,要注意“两定”:一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;二是定方向,定方向的原则是:“小于向左,大于向右”.

练习册系列答案
相关题目
20.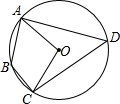 如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )
 如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
1.关于x的一元一次方程(a-1)x2+x+a2-1=0的一个解是0,则a的值为( )
| A. | 1 | B. | -l | C. | 1 或-1 | D. | 2 |
 如图所示,网格中有△ABC和点D,请你找出另外两点E、F,在图中画出△DEF,使△ABC≌△DEF,且顶点A、B、C分别与D、E、F对应.
如图所示,网格中有△ABC和点D,请你找出另外两点E、F,在图中画出△DEF,使△ABC≌△DEF,且顶点A、B、C分别与D、E、F对应.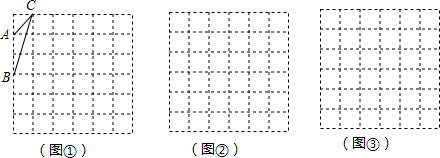
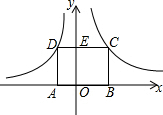 如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.
如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.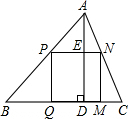 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件PQMN,使正方形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.求这个正方形零件PQMN面积S.
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件PQMN,使正方形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.求这个正方形零件PQMN面积S.