题目内容
7.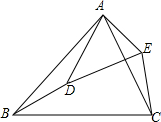 已知:如图,在△ABC和△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.
已知:如图,在△ABC和△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.求证:△ABD∽△ACE.
分析 先根据有两组角对应相等的两个三角形相似得到△ABC∽△ADE,则利用相似三角形的性质得到$\frac{AB}{AD}$=$\frac{AC}{AE}$,再根据比例性质得$\frac{AB}{AC}$=$\frac{AD}{AE}$,接着由∠BAC=∠DAE可判断∠BAD=∠CAE,于是可根据两组对应边的比相等且夹角对应相等的两个三角形相似得到结论.
解答 证明:∵∠BAC=∠DAE,∠ABC=∠ADE.
∴△ABC∽△ADE,
∴$\frac{AB}{AD}$=$\frac{AC}{AE}$,
即$\frac{AB}{AC}$=$\frac{AD}{AE}$,
∵∠BAC=∠DAE,
即∠BAD+∠DAC=∠DAC+∠CAE,
∴∠BAD=∠CAE,
∴△ABD∽△ACE.
点评 本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似.

练习册系列答案
相关题目
17.已知圆的半径为r,圆心到直线a的距离为d,d和r分别是方程x2-7x+10=0的两根,则直线a与圆的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相交或相离 | D. | 相离 |
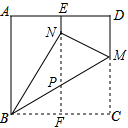 在一张边长为1的正方形纸片ABCD中,对折的折痕为EF,再将点C折到折痕EF上,落在点N的位置,折痕为BH,则EN的长为$\frac{2-\sqrt{3}}{2}$.
在一张边长为1的正方形纸片ABCD中,对折的折痕为EF,再将点C折到折痕EF上,落在点N的位置,折痕为BH,则EN的长为$\frac{2-\sqrt{3}}{2}$.