题目内容
3．判断$\root{3}{5+2\sqrt{13}}$$\root{3}{5-2\sqrt{13}}$是有理数还是无理数．分析 根据根式及平方差公式即可得出原式=-3，由-3为有理数即可得出结论．
解答 解：∵$\root{3}{5+2\sqrt{13}}$•$\root{3}{5-2\sqrt{13}}$=$\root{3}{（5+2\sqrt{13}）（5-2\sqrt{13}）}$=$\root{3}{-27}$=-3．
∴$\root{3}{5+2\sqrt{13}}$•$\root{3}{5-2\sqrt{13}}$为有理数．
点评 本题考查了实数和无理数，通过计算找出$\root{3}{5+2\sqrt{13}}$•$\root{3}{5-2\sqrt{13}}$=-3是解题的关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
14．二次函数y=（x+2）2-3的图象的顶点坐标是（ ）
| A． | （2，3） | B． | （-2，3） | C． | （2，-3） | D． | （-2，-3） |
如图，将一副三角尺的直角顶点叠放在点C处，∠D=30°，∠B=45°，求：
8．一元二次方程x2=4x的根是（ ）
| A． | x=4 | B． | x=2 | C． | x=0或x=4 | D． | x=±2 |
15．我校七年级所有学生参加2017年“元旦联欢晚会”，若每排坐30人，则有8人无座位；若每排坐31人，则空26个座位，则七年级共有多少名学生？设七年级共有x名学生，则所列方程为（ ）
| A． | $\frac{x-8}{30}$=$\frac{x+26}{31}$ | B． | $\frac{x+8}{30}$=$\frac{x-26}{31}$ | C． | $\frac{x}{31}$+8=$\frac{x}{30}$-26 | D． | $\frac{x}{31}$-8=$\frac{x}{30}$+26 |
12．
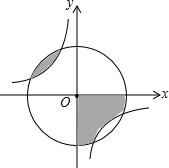如图，反比例函数y=$\frac{k}{x}$（k＜0）的图象与⊙O相交，某同学在⊙O内做随机扎针实验，针头落在阴影区域的概率是（ ）
如图，反比例函数y=$\frac{k}{x}$（k＜0）的图象与⊙O相交，某同学在⊙O内做随机扎针实验，针头落在阴影区域的概率是（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | -$\frac{1}{k}$ | D． | $\frac{1}{π}$ |