题目内容
如图所示，AD是△ABC的中线，E在AC上，BE交AD于点F．当| AF |
| AD |
| 1 |
| 2 |
| AE |
| AC |
考点：平行线分线段成比例,三角形中位线定理
专题：
分析：如图，作辅助线；由DG∥BE得到：
=
=
，故AE=EG；证明EG=CG，即可解决问题．
| AF |
| AD |
| AE |
| AG |
| 1 |
| 2 |
解答：
解：如图，过点D作DG∥BE，交AC于点G；
则
=
=
，
设AE=λ，则EG=λ；
∵BD=DC，DG∥BE，
∴EG=CG=λ，
∴
=
=
．
解：如图，过点D作DG∥BE，交AC于点G；则
| AF |
| AD |
| AE |
| AG |
| 1 |
| 2 |
设AE=λ，则EG=λ；
∵BD=DC，DG∥BE，
∴EG=CG=λ，
∴
| AE |
| AC |
| λ |
| 3λ |
| 1 |
| 3 |
点评：该题主要考查了平行线分线段成比例定理、三角形的中位线定理及其应用问题；解题的关键是作辅助线，灵活运用有关定理来分析、判断．
练习册系列答案
相关题目
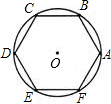如图，在一张圆形纸片上剪下一个面积最大的正六边形纸片ABCDEF，它的边长是24cm， |
| AB |
| A、6πcm | B、8πcm |
| C、36πcm | D、96πcm |
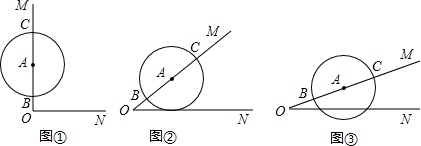
如图所示，AB∥CD，你能探究α、β、γ之间的关系吗？试试看．
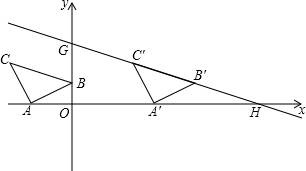
如图，在直角坐标系中，B点的坐标为（a，b），且a，b满足|a+b-4|+（a-2）2=0．