题目内容
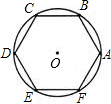如图，在一张圆形纸片上剪下一个面积最大的正六边形纸片ABCDEF，它的边长是24cm， |
| AB |
| A、6πcm | B、8πcm |
| C、36πcm | D、96πcm |
考点：正多边形和圆
专题：
分析：连接OA、OB，得出等边三角形AOB，求出OB长和∠AOB度数，根据弧长公式求出即可．
解答：
解：连接OB、OA，
∵六边形ABCDEF是正六边形，
∴∠AOB=
=60°，
∵OA=OB，
∴△OAB是等边三角形，
∴OB=AB=24cm，
∴
=96π，
故选D．
解：连接OB、OA，∵六边形ABCDEF是正六边形，
∴∠AOB=
| 360° |
| 6 |
∵OA=OB，
∴△OAB是等边三角形，
∴OB=AB=24cm，
∴
| 60π×242 |
| 360 |
故选D．
点评：本题考查了正六边形和圆，弧长公式得应用，解此题的关键是求出∠AOB的度数和求出OB的长．
练习册系列答案
英才计划期末调研系列答案
相关题目
下列事件中，是必然发生的事件是（ ）
| A、打开电视机，正在播放新闻 |
| B、正数大于负数 |
| C、通过长期努力学习，你会成为数学家 |
| D、下雨天，每个人都打着雨伞 |
一个数是8，另一个数比8的相反数小3，则这两个数的和为（ ）
| A、-3 | B、-19 | C、19 | D、3 |
若分式
=0，则a取值为（ ）
| a2-4 |
| a-2 |
| A、a=2 | B、a=-2 |
| C、a=0 | D、a=-2或a=2 |
下列计算错误的是（ ）
A、a（a-
| ||||
| B、（a-2）2=a2-4a+4 | ||||
| C、（a2-2ab+a）÷a=a-2b+1 | ||||
| D、（a+2）（a-3）=a2-6 |
如图，已知△ABC，作一条与BC平行的直线，把△ABC划分成两部分．要使划分成的三角形与四边形的面积之比为1：2，可怎样做？如果要使划分成的两部分的面积之比为1：n呢？
尺规作图（不写作法，保留作图痕迹）
如图所示，AD是△ABC的中线，E在AC上，BE交AD于点F．当
用边长为1的正方形纸片剪刀出一副七巧板，将其拼成如图的“小天鹅”，则阴影部分的面积是原正方形面积的