题目内容
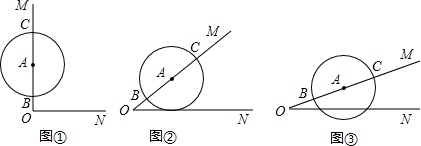
如图①,∠MON=90°,A为射线OM上一点,以A为圆心,r为半径作⊙A交OM于B、C两点,且OB=2
-2,0C=2
+2,
(1)求⊙A的半径r的值.
(2)当射线OM绕点O顺时针旋转45°时,(如图②),判断ON与⊙A的位置关系,并加以证明;
(3)若射线OM绕点O顺时针旋转到如图③位置时,ON与⊙A相较于D、E两点,当DE=2
时,求∠MON的度数.
| 2 |
| 2 |
(1)求⊙A的半径r的值.
(2)当射线OM绕点O顺时针旋转45°时,(如图②),判断ON与⊙A的位置关系,并加以证明;
(3)若射线OM绕点O顺时针旋转到如图③位置时,ON与⊙A相较于D、E两点,当DE=2
| 2 |

考点:圆的综合题
专题:
分析:(1)根据线段的和差,可得圆的直径,根据直径与半径的关系,可得答案;
(2)根据线段的和差,可得OA的长,根据正弦函数,可得AD的长,根据圆的切线的判定,可得答案;
(3)根据垂径定理,可得DF的长,根据勾股定理,可得AF的长,再根据特殊角的三角函数值,可得答案.
(2)根据线段的和差,可得OA的长,根据正弦函数,可得AD的长,根据圆的切线的判定,可得答案;
(3)根据垂径定理,可得DF的长,根据勾股定理,可得AF的长,再根据特殊角的三角函数值,可得答案.
解答:解:(1)由线段的和差,得BC=OC-OB=(2
+2)-(2
-2)=2
+2-2
+2=4,
由r=
d=
×4=2;
(2)ON是⊙A的切线,
证明:如图2:作AD⊥ON与D点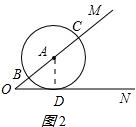 ,
,
∵OB=2
-2,AB=2,
∴OA=OB+AB=2
-2+2=2
.
∵sin∠AOD=sin45°=
=
,
∴
=
,AD=2,
∵AD=2=r,AD⊥ON
∴ON是⊙A的切线;
(3)如图3:作AF⊥DE与F点,连接AD,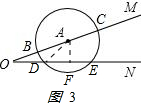 ,
,
由垂径定理,得DF=
DE=
.
在Rt△ADF中,由勾股定理得
AF=
=
=
.
在Rt△OAF中,由正弦函数,得
sin∠O=
=
=
,
∴∠MON=30°.
| 2 |
| 2 |
| 2 |
| 2 |
由r=
| 1 |
| 2 |
| 1 |
| 2 |
(2)ON是⊙A的切线,
证明:如图2:作AD⊥ON与D点
 ,
,∵OB=2
| 2 |
∴OA=OB+AB=2
| 2 |
| 2 |
∵sin∠AOD=sin45°=
| ||
| 2 |
| AD |
| AO |
∴
| ||
| 2 |
| AD | ||
2
|
∵AD=2=r,AD⊥ON
∴ON是⊙A的切线;
(3)如图3:作AF⊥DE与F点,连接AD,
 ,
,由垂径定理,得DF=
| 1 |
| 2 |
| 2 |
在Rt△ADF中,由勾股定理得
AF=
| AD2-DF2 |
22-(
|
| 2 |
在Rt△OAF中,由正弦函数,得
sin∠O=
| AF |
| AO |
| ||
2
|
| 1 |
| 2 |
∴∠MON=30°.
点评:本题考查了圆的综合题,利用了切线的判定定理,圆的垂径定理,锐角三角函数.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
下列命题的逆命题是真命题的是( )
| A、如果两个角都是直角,那么这两个角相等 |
| B、如果三角形中有一个角是直角,那么另外两个角都是锐角 |
| C、全等三角形的三条边对应相等 |
| D、关于某一条直线对称的两个三角形全等 |
下列事件中,是必然发生的事件是( )
| A、打开电视机,正在播放新闻 |
| B、正数大于负数 |
| C、通过长期努力学习,你会成为数学家 |
| D、下雨天,每个人都打着雨伞 |
下列各数中,比-
小的数是( )
| 1 |
| 2 |
| A、1 | ||
| B、0 | ||
C、
| ||
| D、-1 |
下列运算正确的是( )
| A、|-5|=-5 | ||||||
B、(
| ||||||
C、
| ||||||
| D、(-1)3=1 |
一个数是8,另一个数比8的相反数小3,则这两个数的和为( )
| A、-3 | B、-19 | C、19 | D、3 |
若分式
=0,则a取值为( )
| a2-4 |
| a-2 |
| A、a=2 | B、a=-2 |
| C、a=0 | D、a=-2或a=2 |

 如图所示,AD是△ABC的中线,E在AC上,BE交AD于点F.当
如图所示,AD是△ABC的中线,E在AC上,BE交AD于点F.当