题目内容
4．在0，1，2这三个数中任选两个数分别作为P点的横坐标和纵坐标，则P点落在直线y=x+1图象上的概率是$\frac{1}{3}$．分析 先利用树状图展示所有6种等可能的结果数，再根据一次函数图象上点的坐标特征可判断点（0，1）、（1，2）在直线y=x+1上，于是可根据概率公式计算出P点落在直线y=x+1图象上的概率．
解答 解：画树状图为：
共有6种等可能的结果数，其中（0，1）、（1，2）落在直线y=x+1上，
所以P点落在直线y=x+1上的概率=$\frac{2}{6}$=$\frac{1}{3}$．
故答案为$\frac{1}{3}$．
点评 本题考查了列表法与树状图法：通过列表法或树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求事件A或B的概率．也考查了一次函数图象上点的坐标特征．
练习册系列答案
相关题目
14．
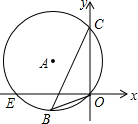如图，⊙A经过点E、B、C、O，且C（0，8），E（-6，0），O（0，0），则cos∠OBC的值为（ ）
如图，⊙A经过点E、B、C、O，且C（0，8），E（-6，0），O（0，0），则cos∠OBC的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{3}{16}$ |
15．
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上，若∠BCA=90°，∠BAC=30°，AB=4cm，则图中阴影部分面积为（ ）
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上，若∠BCA=90°，∠BAC=30°，AB=4cm，则图中阴影部分面积为（ ）| A． | $（{\frac{16}{3}π-2\sqrt{3}}）$cm2 | B． | $（{4π-2\sqrt{3}}）$cm2 | C． | 4πcm2 | D． | $（{4π+2\sqrt{3}}）$cm2 |
如图，ABCD为正方形，O为AC、BD的交点，△DCE为Rt△，∠CED=90°，∠DCE=30°，若OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$，则正方形的面积为4．
如图，△ABC中，∠ABC=90°，F是AC的中点，过AC上一点D作DE∥AB，交BF的延长线于点E，AG⊥BE，垂足是G，连接BD、AE．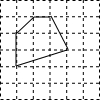
如图，多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形，它的面积S可用公式S=a+$\frac{1}{2}$b-1（a是多边形内的格点数，b是多边形边界上的格点数）计算，这个公式称为“皮克定理”．现用一张方格纸共有200个格点，画有一个格点多边形，它的面积S=40．