题目内容
5. 如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是5.
如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是5.
分析 过O作OC⊥AB于C,根据垂径定理求出AC,根据勾股定理求出OC即可.
解答 解:过O作OC⊥AB于C,
∴AC=BC=$\frac{1}{2}$AB=12,
在Rt△AOC中,由勾股定理得:OC=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
故答案为:5.
点评 本题考查了垂径定理和勾股定理的应用,关键是求出OC的长.

练习册系列答案
相关题目
11.当x=1时,ax+b+1的值为-2,则(a+b-1)(1-a-b)的值为( )
| A. | -16 | B. | -8 | C. | 8 | D. | 16 |
16.把∠A是直角的△ABC绕A点顺时针旋转60度,点B转到点E得△AEF,则下列结论错误的是( )
| A. | ∠BAF=150° | B. | AB=AF | C. | EF=BC | D. | ∠CAF=60° |
13.甲、乙两校参加长沙市教育局举办的科技创新大赛,两校参赛人数相等.比赛结束后,发现学生的成绩分别为7分、8分、9分、10分.依据统计数据绘制了如下尚不完整的统计图表.
甲校成绩统计图:
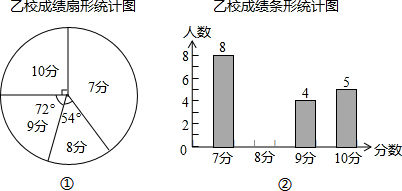
(1)在乙校成绩扇形统计图中,“9分”所在扇形的圆心角等于72°;
(2)请你将乙校成绩条形统计图补充完整;
(3)经计算,甲校的平均分是8.3分,中位数是7分,请写出乙校的平均分和中位数,并从平均分和中位数的角度分析哪个学校成绩较好;
(4)如果市教育局要组织一个8人的代表队参加省级团体赛,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校,并说一说理由.
甲校成绩统计图:
| 分数 | 7分 | 8分 | 9分 | 10分 |
| 人数(人) | 11 | 0 | 8 |

(1)在乙校成绩扇形统计图中,“9分”所在扇形的圆心角等于72°;
(2)请你将乙校成绩条形统计图补充完整;
(3)经计算,甲校的平均分是8.3分,中位数是7分,请写出乙校的平均分和中位数,并从平均分和中位数的角度分析哪个学校成绩较好;
(4)如果市教育局要组织一个8人的代表队参加省级团体赛,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校,并说一说理由.
10.下列四个几何体中,俯视图是圆的几何体共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.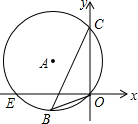 如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )
如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )
 如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )
如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{16}$ |
15. 将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
 将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )| A. | $({\frac{16}{3}π-2\sqrt{3}})$cm2 | B. | $({4π-2\sqrt{3}})$cm2 | C. | 4πcm2 | D. | $({4π+2\sqrt{3}})$cm2 |
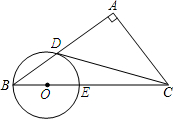 在Rt△ABC中,∠A=90°,点O在BC上,以点O为圆心,OB长为半径的圆与AB、BC分别交于点D、E,且∠ACD=∠B.
在Rt△ABC中,∠A=90°,点O在BC上,以点O为圆心,OB长为半径的圆与AB、BC分别交于点D、E,且∠ACD=∠B.