题目内容
7.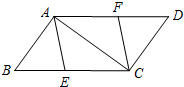 如图,已知E、F分别是?ABCD的边BC、AD上的点,且BE=DF.
如图,已知E、F分别是?ABCD的边BC、AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.
分析 (1)利用平行四边形的性质得出AF∥EC,进而得出AF=EC,进而求出即可;
(2)利用菱形的性质以及三角形内角和定理得出∠1=∠2,进而求出∠3=∠4,再利用直角三角形的性质得出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴AF∥EC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形.
(2)解:∵四边形AECF是菱形,
∴AE=EC,
∴∠1=∠2,
∵∠BAC=90°,
∴∠3=90°-∠2,∠4=90°-∠1,
∴∠3=∠4,
∴AE=BE,
∴BE=AE=CE=$\frac{1}{2}$BC=5.
点评 此题主要考查了平行四边形的性质与判定和菱形的性质与直角三角形的性质,得出∠3=∠4是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
 将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )| A. | $({\frac{16}{3}π-2\sqrt{3}})$cm2 | B. | $({4π-2\sqrt{3}})$cm2 | C. | 4πcm2 | D. | $({4π+2\sqrt{3}})$cm2 |
2.事件A:“若a是实数,则|a|≥a”;事件B:“若实数x满足x>-x,则x正实数”.则下列关于事件A和事件B的说法正确的是( )
| A. | 事件A是必然事件,而事件B是随机事件 | |
| B. | 事件A是随机事件,而事件B是必然事件 | |
| C. | 事件A是必然事件,而事件B是必然事件 | |
| D. | 事件A是随机事件,而事件B是随机事件 |
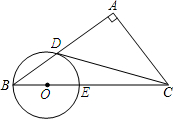 在Rt△ABC中,∠A=90°,点O在BC上,以点O为圆心,OB长为半径的圆与AB、BC分别交于点D、E,且∠ACD=∠B.
在Rt△ABC中,∠A=90°,点O在BC上,以点O为圆心,OB长为半径的圆与AB、BC分别交于点D、E,且∠ACD=∠B.
 如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$,则正方形的面积为4.
如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$,则正方形的面积为4.