题目内容
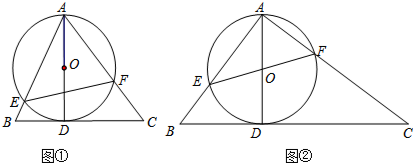
6. 如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
分析 (1)根据等腰三角形的性质由BC=DC得到∠CBD=∠CDB=39°,再根据圆周角定理得∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,所以∠BAD=∠BAC+∠CAD=78°;
(2)根据等腰三角形的性质由EC=BC得∠CEB=∠CBE,再利用三角形外角性质得∠CEB=∠2+∠BAE,则∠2+∠BAE=∠1+∠CBD,加上∠BAE=∠CBD,所以∠1=∠2.
解答 (1)解:∵BC=DC,
∴∠CBD=∠CDB=39°,
∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°;
(2)证明:∵EC=BC,
∴∠CEB=∠CBE,
而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD,
∵∠BAE=∠BDC=∠CBD,
∴∠1=∠2.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰三角形的性质.

练习册系列答案
相关题目
16.把∠A是直角的△ABC绕A点顺时针旋转60度,点B转到点E得△AEF,则下列结论错误的是( )
| A. | ∠BAF=150° | B. | AB=AF | C. | EF=BC | D. | ∠CAF=60° |
14.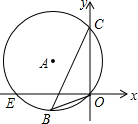 如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )
如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )
 如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )
如图,⊙A经过点E、B、C、O,且C(0,8),E(-6,0),O(0,0),则cos∠OBC的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{16}$ |
15. 将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
 将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )
将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为( )| A. | $({\frac{16}{3}π-2\sqrt{3}})$cm2 | B. | $({4π-2\sqrt{3}})$cm2 | C. | 4πcm2 | D. | $({4π+2\sqrt{3}})$cm2 |
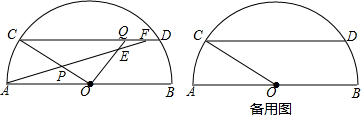
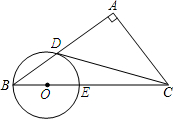 在Rt△ABC中,∠A=90°,点O在BC上,以点O为圆心,OB长为半径的圆与AB、BC分别交于点D、E,且∠ACD=∠B.
在Rt△ABC中,∠A=90°,点O在BC上,以点O为圆心,OB长为半径的圆与AB、BC分别交于点D、E,且∠ACD=∠B.