题目内容
11.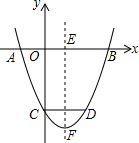 如图,抛物线y=x2-mx+n经过点A(-1,0),与x轴的另一个交点是B(B在A的右侧),与y轴交于点C,抛物线的对称轴EF交x轴于点E,点C关于EF的对称点是点D.
如图,抛物线y=x2-mx+n经过点A(-1,0),与x轴的另一个交点是B(B在A的右侧),与y轴交于点C,抛物线的对称轴EF交x轴于点E,点C关于EF的对称点是点D.(1)n=-m-1(用含m的代数式表示).
(2)当点E是OA中点时,求该抛物线对应的函数关系式.
(3)当以点A,C,D,E为顶点的四边形是平行四边形时,求m的值.
(4)连结AC、CE,当△ACE的面积是$\frac{1}{2}$时,直接写出m的值.
分析 (1)把点A(-1,0)代入抛物线y=x2-mx+n,即可用含m的代数式表示n;
(2)根据抛物线对称轴公式可得抛物线的对称轴是x=$\frac{m}{2}$,再根据中点坐标公式可得gym的方程,解方程即可求得m的值,从而得到该抛物线对应的函数关系式;
(3)分两种情况:①当m>0时,②当-2<m<0时,根据平行四边形的性质可求m的值;
(4)分两种情况:①当m>-1时,②当-2<m<-1时,根据三角形面积公式可求m的值.
解答 解:(1)∵抛物线y=x2-mx+n经过点A(-1,0),
∴1+m+n=0,
∴n=-m-1;
(2)抛物线y=x2-mx-m-1的对称轴是x=$\frac{m}{2}$.
AE=$\frac{m}{2}$+1.
∵点E是OA中点,
∴AE=$\frac{m}{2}$+1=$\frac{1}{2}$.
∴m=-1.
∴抛物线对应的函数关系式为y=x2+x.
(3)①当m>0时,如图①,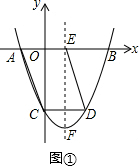
∵抛物线y=x2-mx-m-1的对称轴是x=$\frac{m}{2}$,
∴CD=m,AE=$\frac{m}{2}$+1.
∵四边形ACDE是平行四边形,
∴m=$\frac{m}{2}$+1,
∴m=2;
②当-2<m<0时,如图②,CD=-m,AE=$\frac{m}{2}$+1.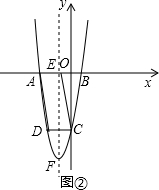
∵四边形ADCE是平行四边形,
∴-m=$\frac{m}{2}$+1.
∴m=-$\frac{2}{3}$;
(4)m=0.解题过程如下:
①当m>-1时,如图③,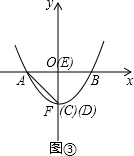
S△ACE=$\frac{1}{2}$AE•OC
=$\frac{1}{2}$($\frac{m}{2}$+1)(m+1)
=$\frac{1}{4}$m2+$\frac{3}{4}$m+$\frac{1}{2}$.
∴$\frac{1}{4}$m2+$\frac{3}{4}$m+$\frac{1}{2}$=$\frac{1}{2}$,
解得m1=0,m2=-3(不合题意,舍去).
∴m=0.
②当-2<m<-1时,如图④,
S△ACE=$\frac{1}{2}$AE•OC
=$\frac{1}{2}$($\frac{m}{2}$+1)(-m-1)
=-$\frac{1}{4}$m2-$\frac{3}{4}$m-$\frac{1}{2}$.
∴-$\frac{1}{4}$m2-$\frac{3}{4}$m-$\frac{1}{2}$=$\frac{1}{2}$,
即m2+3m+4=0,
△=b2-4ac=9-16=-7<0,
∴此方程没有实数根.
综上所述,当m=0时,△ACE的面积是$\frac{1}{2}$.
故答案为:-m-1.
点评 考查了二次函数综合题,解题的关键是熟练掌握抛物线对称轴公式,中点坐标公式,待定系数法求函数关系式,平行四边形的性质,三角形面积的知识点,同时涉及方程思想和分类讨论思想的应用.

| A. | -6 | B. | 0 | C. | -2 | D. | 2 |
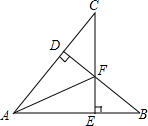 已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线.
已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线. 如图,AC:BC=5:7,AD:BD=5:11,若CD=11cm,则AB=$\frac{528}{5}$cm.
如图,AC:BC=5:7,AD:BD=5:11,若CD=11cm,则AB=$\frac{528}{5}$cm. 如图,点C在线段AB上,D是线段AC的中点,若BD=5cm,BC=2cm,则AB的长度为8cm.
如图,点C在线段AB上,D是线段AC的中点,若BD=5cm,BC=2cm,则AB的长度为8cm.