题目内容
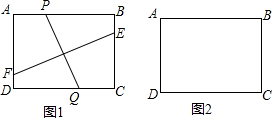
19.如图,在长方形ABCD中,AB=8,AD=6,点P、Q分别是AB边和CD边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP=CQ.线段PQ的垂直平分线与直线BC、AD分别相交与点E、F点.(1)若E、F分别与B、D重合,求AP的长.
(2)当E、F在边BC、AD上时,设AP=x,BE=y,求y与x的函数关系式及x取值范围;
(3)是否存在这样的一点P,使△PQE为直角三角形?若存在,请求出AP的值,若不存在请说明理由.
分析 (1)利用线段垂直平分线的性质结合勾股定理得出AP的长;
(2)利用线段垂直平分线的性质结合勾股定理得出y与x之间的关系进而得出x取值范围;
(3)首先判断只有∠PEQ=90°,得出△PBE≌△ECQ(AAS),进而分析得出答案.
解答 解: (1)如图1,AP=x,则BP=8-x;
(1)如图1,AP=x,则BP=8-x;
∵BD垂直平分PQ;
∴PB=BQ=8-x
Rt△BQC中
(8-x)2=x2+62,
解得:x=$\frac{7}{4}$,则AP=$\frac{7}{4}$;
(2)连接EP、EQ
∵EF垂直平分PQ;
∴EP=EQ
在Rt△PBE和Rt△QCE中
(8-x)2+y2=x2+(6-y)2,
则y=$\frac{4x-7}{3}$,
∵0≤y≤6,
∴$\frac{7}{4}$≤x≤$\frac{25}{4}$;
(3)当E在BC边上,若△PQE为直角三角形,则只有∠PEQ=90°,
∵∠PEQ=90°,
∴∠PEB+∠QEC=90°,
∵∠BPE+∠PEB=90°,
∴∠BPE=∠QEC,
在△PBE和△ECQ中
∵$\left\{\begin{array}{l}{∠B=∠C}\\{∠BPE=QEC}\\{PE=QE}\end{array}\right.$,
∴△PBE≌△ECQ(AAS),
则BE=CQ=x=y,
∵y=$\frac{4x-7}{3}$,
∴解得:x=7,
∵x=7不在定义域范围内,
∴不存在,
当E在边BC(或CB)延长线上时,△PQE每个角都小于90°,不可能为直角三角形,
综上所述,这样的P点不存在.
点评 此题主要考查了四边形综合以及全等三角形的判定与性质和线段垂直平分线的性质等知识,正确利用勾股定理得出y与x之间的关系是解题关键.

练习册系列答案
相关题目
10.为了发展农村经济,政府决定从2011年起,鼓励农民种植果树.并出台了一项奖励措施:在种植过程中,每一年新增面积达到10亩的农户,可得到1500元生活补贴,且每超出一亩,政府还给予m元的奖励,另外种植果树后的土地从下一年起,果实即可出售,且平均每亩可获得200元的收入.如表是某农户头两年种植果树每年获得总收入情况:
(提示:年总收入=生活补贴+政府奖励+出售果实收入)
(1)根据以上提供的信息求m的值.
(2)如果该农户在2013年新增30亩,那么他2013年的年总收入是多少?
(3)现政府规定若收入超过1万元,则取消生活补助,并且超出部分需缴纳10%的个人所得税,从2012年起,如果该农户每年增加的新增面积均能按相同的亩数增长,那么2014年该农户总收入是多少?
| 年份 | 新增亩数 | 总收入 |
| 2011 | 20 | 2400元 |
| 2012 | 26 | 6940元 |
(1)根据以上提供的信息求m的值.
(2)如果该农户在2013年新增30亩,那么他2013年的年总收入是多少?
(3)现政府规定若收入超过1万元,则取消生活补助,并且超出部分需缴纳10%的个人所得税,从2012年起,如果该农户每年增加的新增面积均能按相同的亩数增长,那么2014年该农户总收入是多少?
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有4个.
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有4个.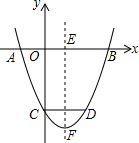 如图,抛物线y=x2-mx+n经过点A(-1,0),与x轴的另一个交点是B(B在A的右侧),与y轴交于点C,抛物线的对称轴EF交x轴于点E,点C关于EF的对称点是点D.
如图,抛物线y=x2-mx+n经过点A(-1,0),与x轴的另一个交点是B(B在A的右侧),与y轴交于点C,抛物线的对称轴EF交x轴于点E,点C关于EF的对称点是点D.