题目内容
6.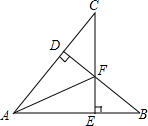 已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线.
已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线.
分析 由条件可以先证明△CFD≌△BEF,可得DF=FE,再结合AF=AF,可证明Rt△ADF≌Rt△AEF,可得∠DAF=∠EAF,可得结论.
解答 证明:∵CE⊥AB,BD⊥AC,
∴∠CDF=∠BEF,
在△CFD和△BEF中,
$\left\{\begin{array}{l}{∠CDF=∠BEF}\\{∠CFD=∠BFE}\\{BF=CF}\end{array}\right.$,
∴△CFD≌△BEF(AAS),
∴DF=EF,
在Rt△ADF和Rt△AEF中,
$\left\{\begin{array}{l}{DF=EF}\\{AF=AF}\end{array}\right.$,
∴Rt△ADF≌Rt△AEF(HL),
∴∠CAF=∠BAF,
∴AF为∠BAC的平分线.
点评 本题主要考查三角形全等的判定和性质,正确掌握三角形全等的判定方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知等边三角形的边长为a,则它边上的高、面积分别是( )
| A. | $\frac{a}{2}$,$\frac{{a}^{2}}{4}$ | B. | $\frac{\sqrt{3}a}{2}$,$\frac{{a}^{2}}{4}$ | C. | $\frac{\sqrt{3}a}{2}$,$\frac{\sqrt{3}{a}^{2}}{4}$ | D. | $\frac{3a}{4}$,$\frac{\sqrt{3}{a}^{2}}{4}$ |
18.已知多项式:A=2a2+ab-2a-1,B=a2+ab-1.
(1)当a=-$\frac{1}{2}$,b=4时,求A-2B的值;
(2)若多项式C满足:C=A-2B-C,试用a、b的代数式表示C.
(1)当a=-$\frac{1}{2}$,b=4时,求A-2B的值;
(2)若多项式C满足:C=A-2B-C,试用a、b的代数式表示C.
15.下列计算正确的是( )
| A. | 2a+3b=5ab | B. | 5x2-2x2=3 | C. | 4mn-4=mn | D. | -y2-y2=-2y2 |
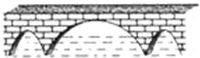 如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为20m,顶点距水面6m,小孔顶点距水面4.5m.当水位上涨刚好淹没小孔时,大孔的水面宽度为10m.
如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为20m,顶点距水面6m,小孔顶点距水面4.5m.当水位上涨刚好淹没小孔时,大孔的水面宽度为10m.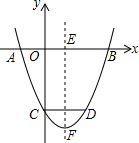 如图,抛物线y=x2-mx+n经过点A(-1,0),与x轴的另一个交点是B(B在A的右侧),与y轴交于点C,抛物线的对称轴EF交x轴于点E,点C关于EF的对称点是点D.
如图,抛物线y=x2-mx+n经过点A(-1,0),与x轴的另一个交点是B(B在A的右侧),与y轴交于点C,抛物线的对称轴EF交x轴于点E,点C关于EF的对称点是点D. 如图所示,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
如图所示,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.