题目内容
 如图,点A在反比例函数y=
如图,点A在反比例函数y=| k |
| x |
(1)求反比例函数y=
| k |
| x |
(2)在y轴上是否存在点P,使得△AOP是直角三角形?若存在,直接写出P点坐标;若不存在,请说明理由.
考点:待定系数法求反比例函数解析式,反比例函数的性质
专题:
分析:(1)把A(2,-4)代入y=
,即可求得k的值,从而求得函数的解析式;
(2)分∠OPA=90°和∠OAP=90°,两种情况进行讨论即可求解.
| k |
| x |
(2)分∠OPA=90°和∠OAP=90°,两种情况进行讨论即可求解.
解答: 解:(1)把A(2,-4)代入y=
解:(1)把A(2,-4)代入y=
得:-4=
,
解得:k=-8,
则函数的解析式是:y=-
;
(2)当∠OPA=90°时,AP⊥y轴,则P的坐标是(0,-4),
当∠OAP=90°时,
根据OA2=4OP,
则20=4OP,
∴OP=5,
则P的坐标是(0,-5).
则P的坐标是(0,-4)或(0,-5).
 解:(1)把A(2,-4)代入y=
解:(1)把A(2,-4)代入y=| k |
| x |
| k |
| 2 |
解得:k=-8,
则函数的解析式是:y=-
| 8 |
| x |
(2)当∠OPA=90°时,AP⊥y轴,则P的坐标是(0,-4),
当∠OAP=90°时,
根据OA2=4OP,
则20=4OP,
∴OP=5,
则P的坐标是(0,-5).
则P的坐标是(0,-4)或(0,-5).
点评:本题考查了反比例函数图象上点的坐标特征,经过函数的某点一定在函数的图象上.

练习册系列答案
相关题目
 如图,在平面直角坐标系内,二次函数y=ax2+bx(a≠0),一次函数y=ax+b以及反比例函数y=
如图,在平面直角坐标系内,二次函数y=ax2+bx(a≠0),一次函数y=ax+b以及反比例函数y=| k |
| x |
| A、b=-4a |
| B、a+b=k |
| C、8a+4b>k |
| D、a+2b>4k |

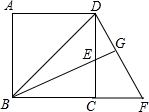 如图,在正方形ABCD中,E是CD上一点,DF⊥BE交BE的延长线于点G,交BC的延长线于点F.
如图,在正方形ABCD中,E是CD上一点,DF⊥BE交BE的延长线于点G,交BC的延长线于点F. 如图,某飞艇于空中A处探测到目标C,此时飞行高度AC=1200米,从飞艇上看地面控制点B的俯角a=30°,求飞艇A到控制点B的距离AB.
如图,某飞艇于空中A处探测到目标C,此时飞行高度AC=1200米,从飞艇上看地面控制点B的俯角a=30°,求飞艇A到控制点B的距离AB.