题目内容
10.已|x-1|=2,求$\sqrt{{x}^{2}-8x+16}$-$\sqrt{4{x}^{2}-4x+1}$的值.分析 首先利用绝对值的性质得出x的值,再利用二次根式的性质化简求出答案.
解答 解:∵|x-1|=2,
∴x-1=±2,
解得:x=3或-1,
∴$\sqrt{{x}^{2}-8x+16}$-$\sqrt{4{x}^{2}-4x+1}$
=$\sqrt{(x-4)^{2}}$-$\sqrt{(2x-1)^{2}}$
当x=3时,原式=1-5=-4;
当x=-1时,原式=5-3=2.
点评 此题主要考查了二次根式的性质与化简以及绝对值的性质,正确得出x的值是解题关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
2.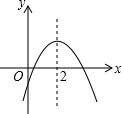 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )| A. | a<0 | B. | b>0 | ||
| C. | c<0 | D. | 当x>0时,y随x增大而增大 |
 如图,以正方形ABCD的对角线BD为边作等边三角形BDE,过E作EF⊥AD,交DA的延长线于F,则∠AEF的度数为45°;若等边三角形BDE的面积为18$\sqrt{2}$cm2,则正方形的面积为12$\sqrt{6}$cm2.
如图,以正方形ABCD的对角线BD为边作等边三角形BDE,过E作EF⊥AD,交DA的延长线于F,则∠AEF的度数为45°;若等边三角形BDE的面积为18$\sqrt{2}$cm2,则正方形的面积为12$\sqrt{6}$cm2.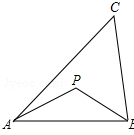 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.举例:如图,若PA=PB,则点P为△ABC的准外心.
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.举例:如图,若PA=PB,则点P为△ABC的准外心.