题目内容
1. 如图,以正方形ABCD的对角线BD为边作等边三角形BDE,过E作EF⊥AD,交DA的延长线于F,则∠AEF的度数为45°;若等边三角形BDE的面积为18$\sqrt{2}$cm2,则正方形的面积为12$\sqrt{6}$cm2.
如图,以正方形ABCD的对角线BD为边作等边三角形BDE,过E作EF⊥AD,交DA的延长线于F,则∠AEF的度数为45°;若等边三角形BDE的面积为18$\sqrt{2}$cm2,则正方形的面积为12$\sqrt{6}$cm2.
分析 由△EAD≌△EAB得∠EAD=∠EAB=$\frac{360°-∠DAB}{2}$=135°,求出∠EAF的值即可求出∠AEF,根据等边三角形的面积公式S△BDE=$\frac{\sqrt{3}}{4}$•(BD)2,求出BD2,再根据正方形面积等于对角线乘积的一半即可解决.
解答  解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠BAF=90°,
∵△BDE是等边三角形,
∴ED=EB=BD,
在△EAD和△EAB中,
$\left\{\begin{array}{l}{ED=EB}\\{AE=AE}\\{AD=AB}\end{array}\right.$,
∴△EAD≌△EAB,
∴∠EAD=∠EAB=$\frac{360°-∠DAB}{2}$=135°,
∴∠EAF=∠EAB-∠BAF=45°,
∵EF⊥DF,
∴∠EFA=90°,
∴∠AEF=90°-∠EAF=45°,
∵S△BDE=$\frac{\sqrt{3}}{4}$(BD)2=18$\sqrt{2}$,
∴BD2=24$\sqrt{6}$,
∴S正方形ABCD=$\frac{1}{2}$•(BD)2=12$\sqrt{6}$.
故答案分别为45°.,12$\sqrt{6}$.
点评 本题考查正方形的性质、等边三角形的性质,全等三角形的判定和性质,需要记住等边三角形的面积公式$\frac{\sqrt{3}}{4}$a2,正方形的面积等于对角线乘积的一半,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.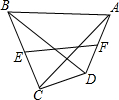 如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
 如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 6 | D. | $\frac{3}{2}\sqrt{3}$ |
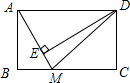 如图,矩形ABCD中,AB=4,AD=9,点M在BC上,且BM:MC=1:2,DE⊥AM于点E,求DE的长为$\frac{36}{5}$.
如图,矩形ABCD中,AB=4,AD=9,点M在BC上,且BM:MC=1:2,DE⊥AM于点E,求DE的长为$\frac{36}{5}$. 如图,把一根底面半径为2dm,高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是多少平方分米?
如图,把一根底面半径为2dm,高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是多少平方分米?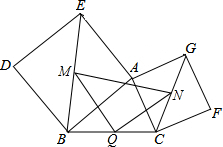 如图,在△ABC的两边AB、AC向形外作正方形ABDE和ACFG,取BE、BC、CG的中点M、Q、N.求证:MQ=QN.
如图,在△ABC的两边AB、AC向形外作正方形ABDE和ACFG,取BE、BC、CG的中点M、Q、N.求证:MQ=QN.