题目内容
1.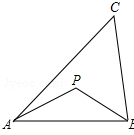 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.举例:如图,若PA=PB,则点P为△ABC的准外心.
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.举例:如图,若PA=PB,则点P为△ABC的准外心.已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,求PA的长.(自己画图)
分析 先利用勾股定理计算出AC=4,根据准外心分类讨论:当PA=PC时,易得PA=$\frac{1}{2}$AC=2,当PA=PC时,设PA=x,则PC=PB=4-x,利用勾股定理得x2+32=(4-x)2,解得x=$\frac{8}{7}$,然后解方程求出x即可.
解答 解:如图,AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,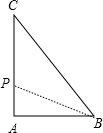
当PA=PC时,PA=$\frac{1}{2}$AC=2,
当PA=PC时,设PA=x,则PC=PB=4-x,
在Rt△ABP中,x2+32=(4-x)2,解得x=$\frac{8}{7}$,即AP的长为$\frac{8}{7}$,
综上所述,AP的长为2或$\frac{8}{7}$.
点评 本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.也考查了阅读理解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.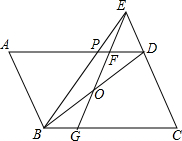 如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.
如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.
(1)求证:DF=BG;
(2)若AB=6,AD=9,求DF的长.
 如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.
如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.(1)求证:DF=BG;
(2)若AB=6,AD=9,求DF的长.
13.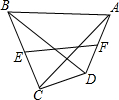 如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
 如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 6 | D. | $\frac{3}{2}\sqrt{3}$ |
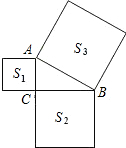 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边向外作正方形,S1、S2、S3分别表示这三个正方形的面积,S1=4,S3=25,则S2=21.
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边向外作正方形,S1、S2、S3分别表示这三个正方形的面积,S1=4,S3=25,则S2=21.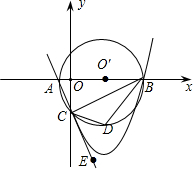 如图,已知A(-1,0),B(9,0),以AB为直径的圆P交y轴负半轴于C,连接AC,BC,
如图,已知A(-1,0),B(9,0),以AB为直径的圆P交y轴负半轴于C,连接AC,BC,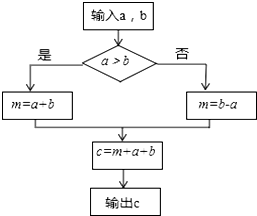 已知a、b为两个不相等的有理数,根据流程图中的程序:
已知a、b为两个不相等的有理数,根据流程图中的程序: