题目内容
2.设x1、x2是方程x2+px+q=0的两个实数根,△是方程的判别式,则△与两根的关系为△=(x1-x2)2.分析 根据根与系数的关系和判别式公式得到x1+x2=-p,x1x2=q,△=b2-4ac=p2-4q,代入化简即可得到结论.
解答 解:∵方程x2+px+q=0的二次项系数a=1,一次项系数b=p,常数项c=q,
∴x1+x2=-p,x1x2=q,△=b2-4ac=p2-4q,
∴△=(x1+x2)2-4x1x2=(x1-x2)2.
故答案是:△=(x1-x2)2.
点评 本题主要考查了一元二次方程的根的判别式△=b2-4ac,根与系数的关系,熟记x1+x2=-$\frac{a}{b}$,x1x2=$\frac{c}{a}$是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
13.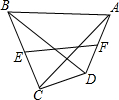 如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
 如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 6 | D. | $\frac{3}{2}\sqrt{3}$ |
14.某个体商贩在一次买卖中,同时卖出两件上衣,每件都以135元出售,若按成本计算,其中一件盈利25%,另一件亏本25%,则在这次买卖中,他( )
| A. | 不赚不赔 | B. | 赔了12元 | C. | 赔了18元 | D. | 赚了18元 |
 如图,把一根底面半径为2dm,高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是多少平方分米?
如图,把一根底面半径为2dm,高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是多少平方分米?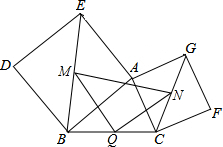 如图,在△ABC的两边AB、AC向形外作正方形ABDE和ACFG,取BE、BC、CG的中点M、Q、N.求证:MQ=QN.
如图,在△ABC的两边AB、AC向形外作正方形ABDE和ACFG,取BE、BC、CG的中点M、Q、N.求证:MQ=QN.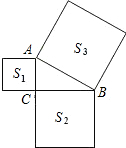 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边向外作正方形,S1、S2、S3分别表示这三个正方形的面积,S1=4,S3=25,则S2=21.
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边向外作正方形,S1、S2、S3分别表示这三个正方形的面积,S1=4,S3=25,则S2=21.