题目内容
15.设关于x的方程mx2+(m2-10)x+2m+6=0有整数根,求整数m.分析 设两个根为x1,x2,所以x1+x2=$\frac{10-{m}^{2}}{m}$=$\frac{10}{m}-m$,x1•x2=$\frac{2m+6}{m}$=2+$\frac{6}{m}$,根据x1、x2为整数,即可确定m的整数值,注意考虑△>0.
解答 解:设两个根为x1,x2,
∵x1+x2=$\frac{10-{m}^{2}}{m}$=$\frac{10}{m}-m$,x1•x2=$\frac{2m+6}{m}$=2+$\frac{6}{m}$,
又∵x1、x2为整数,
∴x1+x2与x1•x2都是整数
∴m=±1或±2,
当m=2时,△<0不合题意,
∴整数m为±1或-2.
点评 本题考查根的判别式、根与系数的关系等知识,学会讨论一个代数式的值是整数的字母的取值,属于中考常考题型.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
5.估计$\sqrt{10}$的值在哪两个整数之间( )
| A. | 9和10 | B. | 7和8 | C. | 5和6 | D. | 3和4 |
6.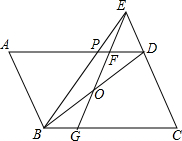 如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.
如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.
(1)求证:DF=BG;
(2)若AB=6,AD=9,求DF的长.
 如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.
如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.(1)求证:DF=BG;
(2)若AB=6,AD=9,求DF的长.
7. 如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.若$\frac{BE}{FB}$=$\frac{5}{8}$,则$\frac{CB}{AD}$的值为( )
如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.若$\frac{BE}{FB}$=$\frac{5}{8}$,则$\frac{CB}{AD}$的值为( )
 如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.若$\frac{BE}{FB}$=$\frac{5}{8}$,则$\frac{CB}{AD}$的值为( )
如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.若$\frac{BE}{FB}$=$\frac{5}{8}$,则$\frac{CB}{AD}$的值为( )| A. | $\frac{5}{16}$ | B. | $\frac{5}{8}$ | C. | 1 | D. | $\frac{5}{4}$ |
 如图,在?ABCD中,AE⊥BC,AF⊥DC交DC的延长线于F,AF=30cm,AE=15cm,∠EAF=30°,求S?ABCD.
如图,在?ABCD中,AE⊥BC,AF⊥DC交DC的延长线于F,AF=30cm,AE=15cm,∠EAF=30°,求S?ABCD.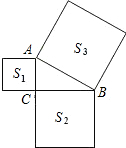 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边向外作正方形,S1、S2、S3分别表示这三个正方形的面积,S1=4,S3=25,则S2=21.
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边向外作正方形,S1、S2、S3分别表示这三个正方形的面积,S1=4,S3=25,则S2=21.