题目内容
13.已知四边形ABCD中,BC∥AD,∠BCD=90°,DE⊥AB于E,AD=CD=4,BC=3(1)如图1,求AE•AB的值;
(2)如图2,连接AC,交DE于点F,求证:CF=4AF;
(3)如图3,连接CE,求sin∠CEB的值.
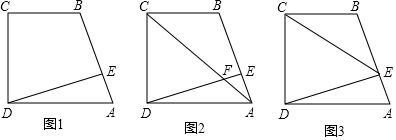
分析 (1)如图1中,作BM⊥AD于M交DE于O.则四边形BCDM是矩形,BC=DM=3,由△ADE∽△ABM,可得$\frac{AD}{AB}$=$\frac{AE}{AM}$,推出AE•AB=AM•AD=1×4=4.
(2)如图2中,作BM⊥AD于M,AN⊥AD交DE的延长线于N.只要证明△ABM≌△DNA,推出AM=AN=1,由AN∥CD,推出$\frac{CF}{AF}$=$\frac{CD}{AN}$=$\frac{4}{1}$,即可解决问题.
(3)如图3中,连接BD,延长DC交AB的延长线于M.由△MCB∽△MED,推出$\frac{MC}{ME}$=$\frac{MB}{MD}$,推出$\frac{MC}{MB}$=$\frac{ME}{MD}$,又∠M=∠M,推出△MBD∽△MCE,推出∠MEC=∠MDB,推出sin∠CEB=sin∠CDB=$\frac{BC}{BD}$,即可解决问题.
解答 解:(1)如图1中,作BM⊥AD于M交DE于O.则四边形BCDM是矩形,BC=DM=3,.
∵DE⊥AB,
∴∠OMD=∠OEB,
∵∠BOE=∠DOM,
∴∠ODM=∠OBE,
∵∠A=∠A,
∴△ADE∽△ABM,
∴$\frac{AD}{AB}$=$\frac{AE}{AM}$,
∴AE•AB=AM•AD=1×4=4.
(2)如图2中,作BM⊥AD于M,AN⊥AD交DE的延长线于N.
∵四边形BCDM是矩形,
∴BM=CD=AD,
∵∠ABM=∠ADN,∠AMB=∠DAN=90°,
∴△ABM≌△DNA,
∴AM=AN=1,
∵AN∥CD,
∴$\frac{CF}{AF}$=$\frac{CD}{AN}$=$\frac{4}{1}$,
∴CF=4AF.
(3)如图3中,连接BD,延长DC交AB的延长线于M.
∵∠M=∠M,∠MCB=∠MED,
∴△MCB∽△MED,
∴$\frac{MC}{ME}$=$\frac{MB}{MD}$,
∴$\frac{MC}{MB}$=$\frac{ME}{MD}$,∵∠M=∠M,
∴△MBD∽△MCE,
∴∠MEC=∠MDB,
∴sin∠CEB=sin∠CDB=$\frac{BC}{BD}$,
在Rt△DBC中,BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴sin∠CEB=$\frac{3}{5}$.
点评 本题考查四边形综合题、直角梯形的性质、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理、锐角三角函数、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形或特殊四边形解决问题,属于中考压轴题.

| A. | 0除以任何数都得0 | |
| B. | 若a<-1,则$\frac{1}{a}$<a | |
| C. | 同号两数相除,取原来的符号,并把两数的绝对值相除 | |
| D. | 若0<a<1,则$\frac{1}{a}$>a |
| A. | -11 | B. | -8 | C. | 4 | D. | 7 |
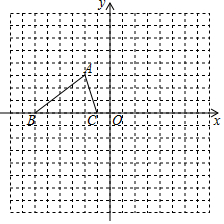 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).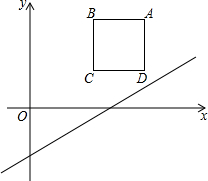 如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AD∥y轴,点A的坐标为(5,3),已知直线l:y=$\frac{1}{2}$x-2.
如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AD∥y轴,点A的坐标为(5,3),已知直线l:y=$\frac{1}{2}$x-2.
 如图,已知抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),与y轴交于点C,点D是抛物线在第一象限的点.
如图,已知抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),与y轴交于点C,点D是抛物线在第一象限的点.