题目内容
18.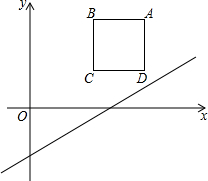 如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AD∥y轴,点A的坐标为(5,3),已知直线l:y=$\frac{1}{2}$x-2.
如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AD∥y轴,点A的坐标为(5,3),已知直线l:y=$\frac{1}{2}$x-2.(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值;
(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.
分析 (1)根据直线平移的规律,可设平移后的直线解析式为y=$\frac{1}{2}$x+b,把点A(5,3)代入,求出b=$\frac{1}{2}$,得到平移后的直线解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$,进而求出m=$\frac{1}{2}$-(-2)=$\frac{5}{2}$;
(2)先求出点E的横坐标为5-2=3,再把x=3代入y=$\frac{1}{2}$x+$\frac{1}{2}$,那么点E的坐标为(3,2),BE=1,根据三角形面积公式即可求出△ABE的面积.
解答 解:(1)设平移后的直线解析式为y=$\frac{1}{2}$x+b,
∵y=$\frac{1}{2}$x+b过点A(5,3),
∴3=$\frac{1}{2}$×5+b,∴b=$\frac{1}{2}$,
∴平移后的直线解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$,
∴m=$\frac{1}{2}$-(-2)=$\frac{5}{2}$;
(2)∵正方形ABCD中,AD∥y轴,点A的坐标为(5,3),
∴点E的横坐标为5-2=3.
把x=3代入y=$\frac{1}{2}$x+$\frac{1}{2}$,得y=$\frac{1}{2}$×3+$\frac{1}{2}$=2,
∴点E的坐标为(3,2),
∴BE=1,
∴△ABE的面积=$\frac{1}{2}$×2×1=1.
点评 本题考查了一次函数图象与几何变换,一次函数图象上点的坐标特征,正方形的性质,三角形的面积,正确求出平移后的直线解析式是解题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
8.下列表示89的含义的是( )
| A. | 9个8相乘 | B. | 9个8相加 | C. | 8个9相乘 | D. | 8个9相加 |
6.下列调查中,适宜采用全面调查(普查)方式的是( )
| A. | 了解我国民众对“乐天萨德事件”的看法 | |
| B. | 了解浙江卫视“奔跑吧兄弟”节目的收视率 | |
| C. | 调查我校某班学生喜欢上数学课的情况 | |
| D. | 调查某类烟花爆竹燃放的安全情况 |
10.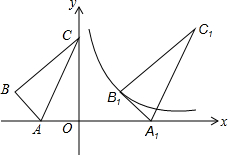 如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )
如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )
 如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )
如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )| A. | (3,2) | B. | (5,6) | C. | (8,6) | D. | (6,6) |
7.如果x-2y=5,xy=-2,那么(x+2y)2=( )
| A. | 17 | B. | 21 | C. | 23 | D. | 9 |
17. 如图,在△ABC中∠A=80°.点D是BC延长线上一点,∠ACD=150°,则∠B=( )
如图,在△ABC中∠A=80°.点D是BC延长线上一点,∠ACD=150°,则∠B=( )
 如图,在△ABC中∠A=80°.点D是BC延长线上一点,∠ACD=150°,则∠B=( )
如图,在△ABC中∠A=80°.点D是BC延长线上一点,∠ACD=150°,则∠B=( )| A. | 60° | B. | 50° | C. | 70° | D. | 165° |
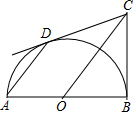 如图所示,AB是半圆O的直径,∠ABC=90°,点D是半圆O上一动点(不与点A、B重合),且AD∥CO.
如图所示,AB是半圆O的直径,∠ABC=90°,点D是半圆O上一动点(不与点A、B重合),且AD∥CO.