题目内容
9. 在平面直角坐标系中,点C的坐标为(2,2),将直角三角尺绕直角顶点C进行旋转,两条直角边分别与x轴正半轴,y轴交于点A,点B.
在平面直角坐标系中,点C的坐标为(2,2),将直角三角尺绕直角顶点C进行旋转,两条直角边分别与x轴正半轴,y轴交于点A,点B.(1)如图,当B与O重合时,试说明:AC=BC;
(2)在旋转过程中,AC=BC这个结论还成立吗?请说明理由;
(3)在旋转的过程中,设A(a,0),B(0,b),请用含a的代数式表示b.
分析 (1)过点C作CD⊥x轴于点D,知AD=BD=2,由点C坐标可得∠CBD=∠BCD=45°,继而可得∠CBD=∠CAB=45°,即可得答案;
(2)过点C作CD⊥x轴于点D,CE⊥y轴于点E,根据点C坐标可得四边形ODCE为正方形,从而知CE=CD、∠BCE=∠ACD,再证△BCE≌△ACD即可;
(3)由(2)可知AD=BE,即a-2=2-b,即可得.
解答 解:(1)如图1,过点C作CD⊥x轴于点D,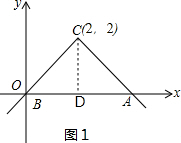
由题意可知AD=BD=2,
∴∠CBD=∠BCD=45°,
∵∠BCA=90°,
∴∠CAB=45°,
∴∠CBD=∠CAB=45°,
∴CB=CA;
(2)如图2,当点B在y轴正半轴上时,过点C作CD⊥x轴于点D,CE⊥y轴于点E,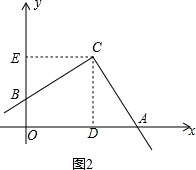
∴∠BOD=∠CDO=∠CEO=90°,
又∵CD=OD=2,
∴四边形ODCE为正方形,
∴CE=CD,
∵∠BCE+∠BCD=∠ACD+∠BCD=90°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
∵$\left\{\begin{array}{l}{∠BCE=∠ACD}\\{CE=CD}\\{∠BEC=∠ADC}\end{array}\right.$,
∴△BCE≌△ACD(ASA),
∴AC=BC;
如图3,当点B在y轴负半轴时,与以上同理可得AC=BC;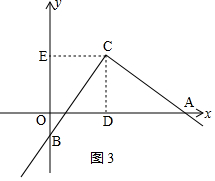
(3)由(2)知,AD=BE,即a-2=2-b,
∴b=4-a.
点评 本题主要考查等腰直角三角形的判定和性质、全等三角形的判定和性质,熟练掌握全等三角形的判定是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
4.某商店举办促销活动,促销的方法是将原价x元的衣服以$\frac{3}{5}$(x-10)元出售,则下列说法中,能正确表达该商店促销方法的是( )
| A. | 原价减去10元后再打6折 | B. | 原价打6折后再减去10元 | ||
| C. | 原价减去10元后再打4折 | D. | 原价打4折后再减去10元 |
5.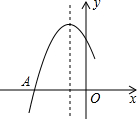 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
①b2>4ac;
②2a+b=0;
③a+b+c>0;
④若B(-5,y1)、C(-1,y2 )为函数图象上的两点,则y1<y2.
其中正确结论是( )
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:①b2>4ac;
②2a+b=0;
③a+b+c>0;
④若B(-5,y1)、C(-1,y2 )为函数图象上的两点,则y1<y2.
其中正确结论是( )
| A. | ②④ | B. | ①③④ | C. | ①④ | D. | ②③ |
14. 如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )
如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )
 如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )
如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )| A. | 随F点运动,其值不变 | B. | 随F点运动而变化,最大值为$\frac{9}{4}$ | ||
| C. | 随F点运动而变化,最小值为$\frac{9}{4}$ | D. | 随F点运动而变化,最小值为$\frac{3}{2}\sqrt{3}$ |
18.如果一个长方形的长减少4cm,宽增加2cm,所得的四边形是一个正方形,且该正方形的面积与原长方形的面积相等,则原长方形的面积为( )
| A. | 8cm2 | B. | 10cm2 | C. | 12cm2 | D. | 16cm2 |