题目内容
18．已知$\sqrt{a-b+4}$+$\sqrt{a+b}$=0，则a2的值为（ ）| A． | 4 | B． | 1 | C． | 0 | D． | -4 |
分析 先依据非负数的性质得到关于a、b的方程组，从而可求得a、b的值，然后依据有理数的乘方法则求解即可．
解答 解：∵$\sqrt{a-b+4}$+$\sqrt{a+b}$=0，
∴a+b=0，a-b+4=0．
∴2a+4=0．
解得：a=-2．
∴a2=4．
故选：A．
点评 本题主要考车的是非负数的性质，依据非负数的性质求得a的值是解题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
8．
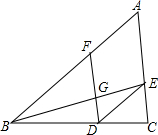在△ABC中，D、F、E分别在边BC、AB、AC上一点，连接BE交FD于点G，若四边形AFDE是平行四边形，则下列说法错误的是（ ）
在△ABC中，D、F、E分别在边BC、AB、AC上一点，连接BE交FD于点G，若四边形AFDE是平行四边形，则下列说法错误的是（ ）| A． | $\frac{AF}{AB}$=$\frac{EG}{BE}$ | B． | $\frac{FG}{GD}$=$\frac{BG}{GE}$ | C． | $\frac{FG}{AB}$=$\frac{DG}{BC}$ | D． | $\frac{AF}{BF}$=$\frac{AE}{BC}$ |
折叠矩形ABCD，使它的顶点D落在BC边上的F处，如图，AB=6，AD=10，那么CE的长为$\frac{8}{3}$．
3．（1）如果直线a∥b，b∥c，那么a∥c
（2）相等的角是对顶角
（3）两条直线被第三条直线所截，同位角相等
（4）在同一平面内如果直线a⊥b，c∥b，那么a∥c
（5）两条直线平行，同旁内角相等；
（6）两条直线相交，所成的四个角中，一定有一个是锐角．
其中真命题有（ ）
（2）相等的角是对顶角
（3）两条直线被第三条直线所截，同位角相等
（4）在同一平面内如果直线a⊥b，c∥b，那么a∥c
（5）两条直线平行，同旁内角相等；
（6）两条直线相交，所成的四个角中，一定有一个是锐角．
其中真命题有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
10．已知|2x-y-3|+（2x+y+11）2=0，则（ ）
| A． | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=0}\\{y=-3}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-1}\\{y=-5}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-2}\\{y=-7}\end{array}\right.$ |
如图，甲、乙两艘轮船同时从港口O出发，甲轮船以20海里/时的速度向南偏东45°方向航行，乙轮船向南偏西45°方向航行．已知它们离开港口O两小时后，两艘轮船相距50海里，求乙轮船平均每小时航行多少海里？
如图，四边形ABCD中，对角线AC，BD相交于点O，AD∥BC，OA=OC，AC平分∠BAD．欲使四边形ABCD是正方形，则还需添加添加AC=BD或∠BAD=90°（写出一个合适的条件即可）