题目内容
9. 折叠矩形ABCD,使它的顶点D落在BC边上的F处,如图,AB=6,AD=10,那么CE的长为$\frac{8}{3}$.
折叠矩形ABCD,使它的顶点D落在BC边上的F处,如图,AB=6,AD=10,那么CE的长为$\frac{8}{3}$.
分析 设CE=x,那么我们可将DE,EC转化到一个三角形中进行计算,根据折叠的性质我们可得出AD=AF,DE=EF,那么DE,CE就都转化到直角三角形EFC中了,下面的关键就是求出FC的长,也就必须求出BF的长,在直角三角形ABF中,已知了AB的长,AF=AD=10,因此可求出BF的长,也就有了CF的长,在直角三角形EFC中,由勾股定理得出方程,解方程即可.
解答 解: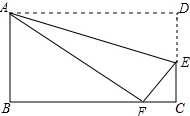 依题意可得:BC=AD=AF=10,DE=EF.
依题意可得:BC=AD=AF=10,DE=EF.
在△ABF中,∠ABF=90°.
∴BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,∴FC=10-8=2,
设CE=x,则EF=DE=6-x.
∵∠C=90°,
∴EC2+FC2=EF2,
∴x2+22=(6-x)2,
解之得:x=$\frac{8}{3}$,
∴CE=$\frac{8}{3}$.
故答案为:$\frac{8}{3}$.
点评 本题考查翻折变换的知识,有一定难度,关键是通过折叠的性质,将所求和已知的线段转换到同一个三角形中是解题的关键.

练习册系列答案
相关题目
19.下列各式运算正确的是( )
| A. | a-(-a)=0 | B. | a+(-a)=0 | C. | a•(-a)=a2 | D. | a÷(-$\frac{1}{a}$)=-1 |
20.下列各运算中,计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 2a+3b=5ab | C. | (-3ab2)2=9a2b4 | D. | (a-b)2=a2-b2 |
17. 如图,CD为⊙O直径,CD⊥AB于点F,AO⊥BC于E,AO=1cm,则阴影部分的面积为( )
如图,CD为⊙O直径,CD⊥AB于点F,AO⊥BC于E,AO=1cm,则阴影部分的面积为( )
 如图,CD为⊙O直径,CD⊥AB于点F,AO⊥BC于E,AO=1cm,则阴影部分的面积为( )
如图,CD为⊙O直径,CD⊥AB于点F,AO⊥BC于E,AO=1cm,则阴影部分的面积为( )| A. | $\frac{1}{3}π$-$\frac{\sqrt{3}}{4}$cm2 | B. | $\frac{\sqrt{3}}{8}$cm2 | C. | $\frac{\sqrt{3}}{2}$cm2 | D. | $\sqrt{3}$cm2 |
4.下列各式属于最简二次根式是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{4}$ | C. | $\sqrt{6}$ | D. | $\sqrt{8}$ |
14.平行四边形ABCD中,∠A比∠B大40°,则∠D的度数为( )
| A. | 60° | B. | 70° | C. | 100° | D. | 110° |
1. 如图所示,若AB∥DC,AD∥BC,则图中与∠A相等(不包括本身)的角有( )个.
如图所示,若AB∥DC,AD∥BC,则图中与∠A相等(不包括本身)的角有( )个.
 如图所示,若AB∥DC,AD∥BC,则图中与∠A相等(不包括本身)的角有( )个.
如图所示,若AB∥DC,AD∥BC,则图中与∠A相等(不包括本身)的角有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.已知$\sqrt{a-b+4}$+$\sqrt{a+b}$=0,则a2的值为( )
| A. | 4 | B. | 1 | C. | 0 | D. | -4 |