题目内容
10.将抛物线y=$\frac{1}{2}$x2-2x+6先向右平移2个单位,再向下平移3个单位后,再将开口反向,所得抛物线的表达式为y=-$\frac{1}{2}$x2+4x-9.分析 把原抛物线写成顶点式形式,求出顶点坐标,再根据向右平移横坐标加,向下平移纵坐标减求出平移后的顶点坐标,写出解析式,然后根据关于x轴对称的两点x坐标相同,y坐标互为相反数,即可得到所求的抛物线的解析式.
解答 解:∵y=$\frac{1}{2}$x2-2x+6=$\frac{1}{2}$(x-2)2+4,
∴原抛物线的顶点坐标为(2,4),
∵向右平移2个单位长度,向下平移3个单位长度,
∴平移后的抛物线顶点坐标为(4,1),
∴平移后的抛物线函数关系式y=$\frac{1}{2}$(x-4)2+1.
∴将开口反向后的函数表达式为:-y=$\frac{1}{2}$(x-4)2+1.即y=-$\frac{1}{2}$x2+4x-9;
故答案为y=-$\frac{1}{2}$x2+4x-9.
点评 本题考查了二次函数图象与几何变换,此类题目利用顶点的平移变换确定抛物线的变换更简单.

练习册系列答案
相关题目
20.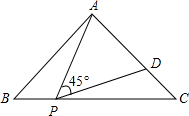 如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )
如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )
 如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )
如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )| A. | 10-3$\sqrt{2}$ | B. | 10-2$\sqrt{3}$ | C. | 4 | D. | 6 |