题目内容
20.已知|3a-b+1|+(3a-$\frac{3}{2}$b)2=0,求$\frac{{b}^{2}}{a+b}$÷[($\frac{b}{a-b}$)2•($\frac{ab}{a+b}$)]的值.分析 先根据非负数的性质求出a、b的值,再根据分式混合运算的法则把原式进行化简,把a、b的值代入进行计算即可.
解答 解:∵|3a-b+1|+(3a-$\frac{3}{2}$b)2=0,
∴$\left\{\begin{array}{l}3a-b+1=0\\ 3a-\frac{3}{2}b=0\end{array}\right.$,解得$\left\{\begin{array}{l}a=-1\\ b=-2\end{array}\right.$.
原式=$\frac{{b}^{2}}{a+b}$÷$\frac{{ab}^{3}}{(a-b)^{2}(a+b)}$
=$\frac{{b}^{2}}{a+b}$•$\frac{(a-{b)}^{2}(a+b)}{{ab}^{3}}$
=$\frac{{(a-b)}^{2}}{a}$,
当a=-1,b=-2时,原式=$\frac{{(-1+2)}^{2}}{-1}$=-1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
6.下列各对数中互为相反数的是( )
| A. | +(-5)和-(+5) | B. | a与-a | C. | π与-3.14 | D. | -(-2.7)与2.7 |
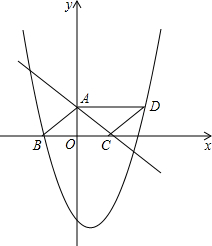 如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B、点D在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且四边形ABCD是平行四边形.
如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B、点D在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且四边形ABCD是平行四边形.