题目内容
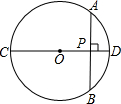 已知:如图,⊙O的直径CD垂直于弦AB,垂足为P,且AP=4cm,PD=2cm,则⊙O的半径为( )
已知:如图,⊙O的直径CD垂直于弦AB,垂足为P,且AP=4cm,PD=2cm,则⊙O的半径为( )| A、4cm | ||
| B、5cm | ||
C、4
| ||
D、2
|
考点:垂径定理,勾股定理
专题:计算题
分析:连结OA,如图,设⊙O的半径为R,由CD⊥AB得到∠APO=90°,在Rt△OAP中根据勾股定理得(r-2)2+42=r2,然后解方程求出r即可.
解答:解: 连结OA,如图,设⊙O的半径为R,
连结OA,如图,设⊙O的半径为R,
∵CD⊥AB,
∴∠APO=90°,
在Rt△OAP中,∵OP=OD-PD=r-2,OA=r,AP=4,
∴(r-2)2+42=r2,解得r=5,
即⊙O的半径为5cm.
故选B.
 连结OA,如图,设⊙O的半径为R,
连结OA,如图,设⊙O的半径为R,∵CD⊥AB,
∴∠APO=90°,
在Rt△OAP中,∵OP=OD-PD=r-2,OA=r,AP=4,
∴(r-2)2+42=r2,解得r=5,
即⊙O的半径为5cm.
故选B.
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD=( )
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD=( )| A、60° | B、90° |
| C、45° | D、75° |
到三角形三个顶点距离相等的点是( )
| A、三角形三条边的垂直平分线的交点 |
| B、三角形三条角平分线的交点 |
| C、三角形三条高的交点 |
| D、三角形三条边的中线的交点 |
 正五边形ABCDE的对角线的长是4,以正五边形的顶点为圆心,对角线长为半径画弧,构造出如图所示的曲边五边形,该曲边五边形的周长是
正五边形ABCDE的对角线的长是4,以正五边形的顶点为圆心,对角线长为半径画弧,构造出如图所示的曲边五边形,该曲边五边形的周长是 如图,直线AB、CD相交于点O,OE⊥AB,如果∠EOD=38°,则∠AOC=
如图,直线AB、CD相交于点O,OE⊥AB,如果∠EOD=38°,则∠AOC= 已知反比例函数y1=
已知反比例函数y1=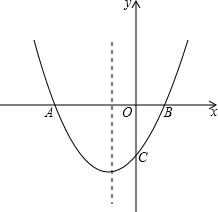 如图抛物线y=x2+2x+1+k与x轴交于A、B两点,与y轴交于点C(0,-3).
如图抛物线y=x2+2x+1+k与x轴交于A、B两点,与y轴交于点C(0,-3).