题目内容
如图，MN是正方形ABCD的一条对称轴，点P是直线MN上的一个动点，当PC+PD最小时，∠PCD=（ ）| A、60° | B、90° |
| C、45° | D、75° |
考点：轴对称-最短路线问题
专题：
分析：根据当PC+PD最小时，作出D点关于MN的对称点，正好是A点，连接AC即可得出∠PCD的度数．
解答：
解：∵当PC+PD最小时，作出D点关于MN的对称点，正好是A点，
连接AC，AC为正方形对角线，根据正方形的性质得出∠PCD=45°，
∴∠PCD=45°．
故选C．
解：∵当PC+PD最小时，作出D点关于MN的对称点，正好是A点，连接AC，AC为正方形对角线，根据正方形的性质得出∠PCD=45°，
∴∠PCD=45°．
故选C．
点评：此题主要考查了轴对称求最短路线问题，根据已知得出D点关于MN的对称点，正好是A点是解题关键．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
如图，直线AB、CD相交于点O．OE平分∠AOD，若∠BOC=70°，则∠AOE的度数是（ ）| A、20° | B、35° |
| C、70° | D、110° |
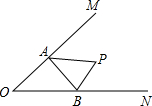如图，已知∠MON=60°，P为∠MON内一点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，∠APB的度数为（ ）度．| A、40 | B、60 |
| C、100 | D、120 |
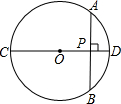已知：如图，⊙O的直径CD垂直于弦AB，垂足为P，且AP=4cm，PD=2cm，则⊙O的半径为（ ）| A、4cm | ||
| B、5cm | ||
C、4
| ||
D、2
|
如图，已知∠α．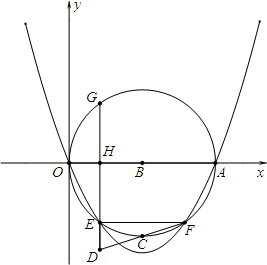
已知A是x轴正半轴上一个动点，以线段OA为直径作⊙B，圆心为点B，直径OA=m，线段EF是⊙B的一条弦，EF∥x轴，点C为劣弧EF的中点，过点E作DE垂直于EF，交抛物线C1：y=ax2+bx（a＞0）于点G，抛物线经过点O和点A．