题目内容
 正五边形ABCDE的对角线的长是4,以正五边形的顶点为圆心,对角线长为半径画弧,构造出如图所示的曲边五边形,该曲边五边形的周长是
正五边形ABCDE的对角线的长是4,以正五边形的顶点为圆心,对角线长为半径画弧,构造出如图所示的曲边五边形,该曲边五边形的周长是考点:正多边形和圆
专题:
分析:找到圆心O,易求得∠AOF的值和OA的长,即可求得AB的长,即可解题.
解答:解:找到圆心O,连接OA,OB,作OF⊥AB交AB于点F,

则∠AOB=
×360°=72°,
∴∠AOF=36°,
∵OA=OB=
×4=2,
∴AB=2AF=2×BO•sin36°=4sin36°,
∴该曲边五边形的周长=5×4sin36°=20sin36°,
故答案为 20sin36°.

则∠AOB=
| 1 |
| 5 |
∴∠AOF=36°,
∵OA=OB=
| 1 |
| 2 |
∴AB=2AF=2×BO•sin36°=4sin36°,
∴该曲边五边形的周长=5×4sin36°=20sin36°,
故答案为 20sin36°.
点评:本题考查了直角三角形中三角函数应用,考查了正多边形各边长相等性质,本题中求得AB的长是解题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
已知4个数中:(-1)2005,|-2|,π,-32,其中正数的个数有( )
| A、1 | B、2 | C、3 | D、4 |
若关于x的方程
-
=0有增根,则a的值是( )
| a-3 |
| x-3 |
| x |
| x-3 |
| A、3 | B、6 | C、-6 | D、-3 |
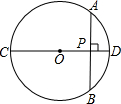 已知:如图,⊙O的直径CD垂直于弦AB,垂足为P,且AP=4cm,PD=2cm,则⊙O的半径为( )
已知:如图,⊙O的直径CD垂直于弦AB,垂足为P,且AP=4cm,PD=2cm,则⊙O的半径为( )| A、4cm | ||
| B、5cm | ||
C、4
| ||
D、2
|
 如图,数轴的单位长度为1,如果点A与点B表示的数是互为相反数,那么点A表示的数是
如图,数轴的单位长度为1,如果点A与点B表示的数是互为相反数,那么点A表示的数是