��Ŀ����
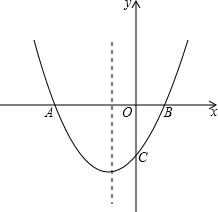 ��ͼ������y=x2+2x+1+k��x�ύ��A��B���㣬��y�ύ�ڵ�C��0��-3����
��ͼ������y=x2+2x+1+k��x�ύ��A��B���㣬��y�ύ�ڵ�C��0��-3������1���������ߵĶԳ��ἰk��ֵ��
��2�������ߵĶԳ������Ƿ����һ��P��ʹ��PB+PC��ֵ��С�������ڣ����ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3����M����������һ���㣬���ڵ������ޣ�
�ٵ�M���˶����δ�ʱ����AMB�������������AMB������������ʱ��M�����ꣻ
�ڵ�M���˶����δ�ʱ���ı���AMCB������������ı���AMCB������������ʱ��M�����꣮
���㣺���κ����ۺ���
ר�⣺
��������1����������y=x2+2x+1+k��y�ύ�ڵ�C��0��-3��������C��������뺯������ʽ��⼴�ɣ�
��2������AC�������ߵĶԳ����ڵ�P����PA+PC��ֵ��С�����A��C�����꣬��ֱ��AC�Ľ���ʽΪy=kx+b�����ô���ϵ�����������ֱ��AC�Ľ���ʽ�������ô�ʱ��P�����ꣻ
��3�������M������Ϊ����x����x+1��2-4�������ɵ�S��AMB=
��4��|��x+1��2-4|���ɶ��κ�������ֵ���⣬������á�AMB������������ʱ��M�����ꣻ
�����M������Ϊ����x����x+1��2-4����Ȼ�����M��MD��AB��D����S�ı���ABCM=S��OBC+S��ADM+S����OCMD�����ݶ��κ�������ֵ�������ⷽ������������ı���AMCB������������ʱ��M�����꣮
��2������AC�������ߵĶԳ����ڵ�P����PA+PC��ֵ��С�����A��C�����꣬��ֱ��AC�Ľ���ʽΪy=kx+b�����ô���ϵ�����������ֱ��AC�Ľ���ʽ�������ô�ʱ��P�����ꣻ
��3�������M������Ϊ����x����x+1��2-4�������ɵ�S��AMB=
| 1 |
| 2 |
�����M������Ϊ����x����x+1��2-4����Ȼ�����M��MD��AB��D����S�ı���ABCM=S��OBC+S��ADM+S����OCMD�����ݶ��κ�������ֵ�������ⷽ������������ı���AMCB������������ʱ��M�����꣮
����⣺��1����������y=��x+1��2+k��y�ύ�ڵ�C��0��-3������-3=1+k��
��k=-4��
�������ߵĽ���ʽΪ��y=��x+1��2-4��
�������ߵĶԳ���Ϊ��x=-1��
��2�����ڣ�
��ͼ1��

����AC�������ߵĶԳ����ڵ�P����PA+PC��ֵ��С��
��y=0ʱ����x+1��2-4=0��
��ã�x=-3��x=1��
��A��B����࣬
��A��-3��0����C��0��-3����
��ֱ��AC�Ľ���ʽΪ��y=kx+b��
��
��
��ã�
��
��ֱ��AC�Ľ���ʽΪ��y=-x-3��
��x=-1ʱ��y=-��-1��-3=-2��
���P����������-1��-2����
��3������ͼ2��

���M����������x����x+1��2-4����
��AB=4��
��S��AMB=
��4��|��x+1��2-4|=2|��x+1��2-4|��
�ߵ�M�ڵ������ޣ�
��S��AMB=8-2��x+1��2��
�൱x=-1ʱ��
����M������Ϊ��-1��-4��ʱ����AMB�����������ֵΪ8��
�����M����������x����x+1��2-4����
��ͼ3������M��MD��AB��D��

S�ı���ABCM=S��OBC+S��ADM+S����OCMD=
��3��1+
����3+x����[4-��x+1��2]+
����-x����[3+4-��x+1��2]��
=-
��x2+3x-4��=-
��x+
��2+
��
��x=-
ʱ��y=��-
+1��2-4=-
��
����M��-
��-
��ʱ���ı���AMCB���������������
��
��k=-4��
�������ߵĽ���ʽΪ��y=��x+1��2-4��
�������ߵĶԳ���Ϊ��x=-1��
��2�����ڣ�
��ͼ1��

����AC�������ߵĶԳ����ڵ�P����PA+PC��ֵ��С��
��y=0ʱ����x+1��2-4=0��
��ã�x=-3��x=1��
��A��B����࣬
��A��-3��0����C��0��-3����
��ֱ��AC�Ľ���ʽΪ��y=kx+b��
��
|
��ã�
|
��ֱ��AC�Ľ���ʽΪ��y=-x-3��
��x=-1ʱ��y=-��-1��-3=-2��
���P����������-1��-2����
��3������ͼ2��

���M����������x����x+1��2-4����
��AB=4��
��S��AMB=
| 1 |
| 2 |
�ߵ�M�ڵ������ޣ�
��S��AMB=8-2��x+1��2��
�൱x=-1ʱ��
����M������Ϊ��-1��-4��ʱ����AMB�����������ֵΪ8��
�����M����������x����x+1��2-4����
��ͼ3������M��MD��AB��D��

S�ı���ABCM=S��OBC+S��ADM+S����OCMD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 75 |
| 8 |
��x=-
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
����M��-
| 3 |
| 2 |
| 15 |
| 4 |
| 75 |
| 8 |
������������Ҫ�����˴���ϵ���������Ľ���ʽ�����κ�������ֵ���⣬���������ı��ε���������Լ��߶κ���������֪ʶ�������ۺ��Խ�ǿ���ѶȽϴ���Ĺؼ��Ƿ���˼�������ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
 �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
�����Ŀ
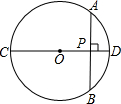 ��֪����ͼ����O��ֱ��CD��ֱ����AB������ΪP����AP=4cm��PD=2cm�����O�İ뾶Ϊ��������
��֪����ͼ����O��ֱ��CD��ֱ����AB������ΪP����AP=4cm��PD=2cm�����O�İ뾶Ϊ��������| A��4cm | ||
| B��5cm | ||
C��4
| ||
D��2
|
����˵����ȷ���ǣ�������
| A������ֵ��С������0 |
| B��ƽ������������������1 |
| C��1������������ |
| D���κ����������е��� |
����˵����ȷ���ǣ�������
| A��-2��-8�������� |
| B��1��ƽ������1 |
| C����-1��2��ƽ������-1 |
| D��16��ƽ������4 |
 ��֪����ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8��ADƽ�֡�CAB����E��б��AB����AC=AE��
��֪����ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8��ADƽ�֡�CAB����E��б��AB����AC=AE��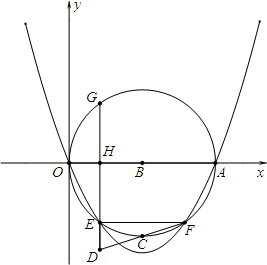 ��֪A��x����������һ�����㣬���߶�OAΪֱ������B��Բ��Ϊ��B��ֱ��OA=m���߶�EF�ǡ�B��һ���ң�EF��x�ᣬ��CΪ�ӻ�EF���е㣬����E��DE��ֱ��EF����������C1��y=ax2+bx��a��0���ڵ�G�������߾�����O�͵�A��
��֪A��x����������һ�����㣬���߶�OAΪֱ������B��Բ��Ϊ��B��ֱ��OA=m���߶�EF�ǡ�B��һ���ң�EF��x�ᣬ��CΪ�ӻ�EF���е㣬����E��DE��ֱ��EF����������C1��y=ax2+bx��a��0���ڵ�G�������߾�����O�͵�A��
