题目内容
12.先化简,再求值.$\frac{{x}^{2}+1}{{x}^{2}-2x+1}$÷($\frac{x}{x-1}$-$\frac{1}{x+1}$),其中x=2.分析 先根据分式混合运算的法则把原式进行化简,再把x=2代入进行计算即可.
解答 解:原式=$\frac{{x}^{2}+1}{(x-1)^{2}}$÷$\frac{x(x+1)-(x-1)}{(x+1)(x-1)}$
=$\frac{{x}^{2}+1}{{(x-1)}^{2}}$÷$\frac{{x}^{2}+x-x+1}{(x+1)(x-1)}$
=$\frac{{x}^{2}+1}{{(x-1)}^{2}}$÷$\frac{{x}^{2}+1}{(x+1)(x-1)}$
=$\frac{{x}^{2}+1}{{(x-1)}^{2}}$•$\frac{(x+1)(x-1)}{{x}^{2}+1}$
=$\frac{x+1}{x-1}$,
当x=2时,原式=$\frac{2+1}{2-1}$=3.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
7.下列命题中,是真命题的是( )
| A. | 任何一个三角形都有且只有一个外接圆 | |
| B. | 任何一组数据的中位数和平均数都不会相等 | |
| C. | 对角线相等且互相垂直的四边形是矩形 | |
| D. | 位似变换不改变图形的形状和大小 |
4.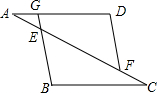 如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
 如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )| A. | $\frac{AG}{AD}=\frac{AE}{AF}$ | B. | $\frac{AG}{AD}=\frac{EG}{DF}$ | C. | $\frac{AE}{AC}=\frac{AG}{AD}$ | D. | $\frac{AD}{BC}=\frac{DF}{BE}$ |
1.下列因式分解正确的是( )
| A. | 9a2-4b2=(3a-2b)2 | B. | -3ab2+6ab=-3ab(b+2) | ||
| C. | $\frac{1}{2}$a2-ab+$\frac{1}{2}$b2=$\frac{1}{2}$(a-b)2 | D. | -a2-b2=-(a+b)(a-b) |
2.下列各式运算正确的是( )
| A. | a3+a2=2a5 | B. | a3-a2=a | C. | (a3)2=a5 | D. | a6÷a3=a3 |