题目内容
观察下面三行数:
①-2,4,-8,16,-32,64,…;
②-1,5,-9,13,-17,21,…;
③-1,4,-9,16,-25,36,…;
(1)第①行第7个数是 写出第n个数.
(2)第②行第7个数是 写出第n个数.
(3)计算第②行与第③行的第10个数的和与第①行第10个数的差.
①-2,4,-8,16,-32,64,…;
②-1,5,-9,13,-17,21,…;
③-1,4,-9,16,-25,36,…;
(1)第①行第7个数是
(2)第②行第7个数是
(3)计算第②行与第③行的第10个数的和与第①行第10个数的差.
考点:规律型:数字的变化类
专题:
分析:(1)观察可看出第一行的数分别是-2的1次方,二次方,三次方,四次方…,用式子表示规律为:(-2)n;
(2)观察第②行的数得出的规律为(-1)n(4n-3);第③行的数得出的规律为(-1)nn2;
(3)写出每一行的第10个数,然后列式计算即可.
(2)观察第②行的数得出的规律为(-1)n(4n-3);第③行的数得出的规律为(-1)nn2;
(3)写出每一行的第10个数,然后列式计算即可.
解答:解:(1)第①行第7个数是-27=-128,第n个数为(-2)n;
(2)第②行第7个数是-25,第n个数(-1)n(4n-3);
(3)第②行的第10个数为4×10-3=37,第③行的第10个数为102,=100,第①行第10个数为210=1024;
则37+100-1024=887.
(2)第②行第7个数是-25,第n个数(-1)n(4n-3);
(3)第②行的第10个数为4×10-3=37,第③行的第10个数为102,=100,第①行第10个数为210=1024;
则37+100-1024=887.
点评:此题考查数字的变化规律,找出数字之间的联系,得出运算规律,利用规律解决问题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
线段AB被分为2:3:4三部分,已知第一部分和第三部分两中点间的距离是5.4cm,则线段AB的长度应为( )
| A、8.1cm |
| B、9.1cm |
| C、10.8cm |
| D、7.4cm |
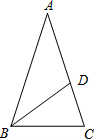 如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.
如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点. 已知AB=AC,AE平分∠DAC,那么AE∥BC吗?为什么?
已知AB=AC,AE平分∠DAC,那么AE∥BC吗?为什么?