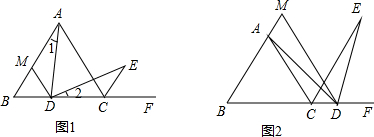题目内容
19．
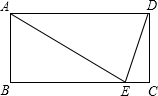已知：如图所示，矩形ABCD中，E是BC上的一点，且AE=BC，∠EDC=15°．求证：AD=2AB．
分析 只要证明∠AEB=30°，即可推出AE=2AB，由此即可证明．
解答 证明：∵四边形ABCD是矩形，
∴∠B=∠ADC=90°，AD∥BC，
∵∠EDC=15°，
∴∠ADE=∠ADC-∠EDC=90°-15°=75°，
∵AE=AD∴∠AED=∠ADE=75°，
∴∠DAE=30°，
∵AD∥BC，
∴∠AEB=∠DAE=30°，
∴AB=$\frac{1}{2}$AE，
∵AD=AE，
∴AD=2AB．
点评 本题参考矩形的性质、等腰三角形的性质等知识，解题的关键是灵活应用这些知识解决问题，属于中考常考题型．
练习册系列答案
相关题目
10．如图，在已知的△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于$\frac{1}{2}$BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠ACB=120°，则∠A的度数为（ ）
①分别以B，C为圆心，以大于$\frac{1}{2}$BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠ACB=120°，则∠A的度数为（ ）
| A． | 60° | B． | 50° | C． | 40° | D． | 不能确定 |
求作：△BAC，使∠ABC=∠ACB=∠α，BC=n．
用圆规、直尺作图，不写作法，但要保留作图痕迹
4．若多项式a2-na-3可以分解成（a+1）（a-3），那么，n应等于（ ）
| A． | 2 | B． | -2 | C． | -1 | D． | 1 |
8．已知△ABC在平面直角坐标系中，点A，B，C都在第一象限内，现将△ABC的三个顶点的横坐标保持不变，纵坐标都乘-1，得到一个新的三角形，则（ ）
| A． | 新三角形与△ABC关于x轴对称 | |
| B． | 新三角形与△ABC关于y轴对称 | |
| C． | 新三角形的三个顶点都在第三象限内 | |
| D． | 新三角形是由△ABC沿y轴向下平移一个单位长度得到的 |
