题目内容
9.如图,△ABC是等边三角形,点D是直线BC上一点,过点D作DM∥AC交直线AB于点M,∠ADE=60°,DE交△ABC的外角∠ACF的平分线CE于点E.(1)如图1,当点D在线段BC上时,求证:∠1=∠2;
(2)如图1,当点D在线段BC上时,求证:AD=DE;
(3)如图2,当点D在BC延长线上时,求证:∠MAD=∠CDE;
(4)如图2,当点D在BC延长线上时,求证:AD=DE.
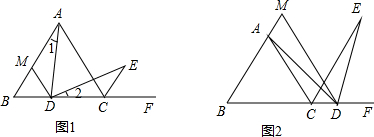
分析 (1)先用三角形的外角和等边三角形的性质即可得出结论;
(2)根据平行线的性质得出∠BDM=60°,结合等边三角形的性质即可得出△BMD是等边三角形,在判断出△AMD≌△DCE即可;
(3)利用三角形的外角即可;
(4)先判断出AM=DC,从而得出△AMD≌△DCE即可得出结论.
解答 (1)证明:∵∠1+∠B=∠ADF
∠2+∠ADE=∠ADF
∴∠1+∠B=∠2+ADE
∵△ABC是等边三角形,
∴∠B=∠ADE=60°
∴∠1=∠2
(2)证明:∵DM∥AC
∴∠BMD=∠BAC=60°
∠BDM=∠BCA=60°
∵∠B=60°
∴∠B=∠BDM=∠BMD
∴△BMD是等边三角形
∴AB-BM=BC-BD
∴AM=DC
在△AMD 和△DCE中$\left\{\begin{array}{l}{∠1=∠2}\\{∠AMD=∠DCE}\\{AM=DC}\end{array}\right.$
∴△AMD≌△DCE(ASA)
∴AD=DE
(3)证明:∵∠MAD=∠B+∠ADC
∠CDE=∠ADE+∠ADC
∠B=∠ADE=60°
∴∠MAD=∠CDE
(4)证明:由(2)知,△BMD是等边三角,
∴BM-AB=BD-BC
∴AM=DC
在△AMD 和△DCE中$\left\{\begin{array}{l}{∠MAD=∠CDE}\\{∠AMD=∠DCE}\\{AM=DC}\end{array}\right.$
∴△AMD≌△DCE(ASA)
∴AD=DE
点评 此题是三角形综合题,主要考查了等边三角形的性质和判定,全等三角形的判定和性质,三角形的外角的性质,平行线的性质,解本题的根据是利用三角形的外角的性质得出∠MAD=∠B+∠ADC.

 阶梯计算系列答案
阶梯计算系列答案| A. | $\frac{π}{3}$ | B. | -0.3 | C. | $\frac{22}{7}$ | D. | $\root{3}{8}$ |
| A. | a4+a4=a8 | B. | a4×a3=a12 | C. | a4÷a3=a | D. | (a4)3=a7 |
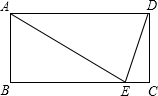 已知:如图所示,矩形ABCD中,E是BC上的一点,且AE=BC,∠EDC=15°.
已知:如图所示,矩形ABCD中,E是BC上的一点,且AE=BC,∠EDC=15°. 如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD于M,且CM=2,则AB的长为8.
如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD于M,且CM=2,则AB的长为8.
 如图,指出数轴上A,B,C,D各点分别表示什么数.
如图,指出数轴上A,B,C,D各点分别表示什么数.