题目内容
 如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知∠B=60°,BD=
如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知∠B=60°,BD=| 3 |
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中阴影部分的面积.
考点:切线的判定,扇形面积的计算
专题:
分析:(1)由AB为圆O的切线,利用切线的性质得到OD垂直于AB,在直角三角形BDO中,利用锐角三角函数定义,根据tan∠B及BD的值,求出OD的值即可;
(2)连接OE,由AE=OD=3,且OD与AE平行,利用一组对边平行且相等的四边形为平行四边形,根据平行四边形的对边平行得到OE与AD平行,再由DA与AE垂直得到OE与AC垂直,即可得证;
(3)阴影部分的面积=三角形BOD的面积-扇形DOF的面积,求出即可.
(2)连接OE,由AE=OD=3,且OD与AE平行,利用一组对边平行且相等的四边形为平行四边形,根据平行四边形的对边平行得到OE与AD平行,再由DA与AE垂直得到OE与AC垂直,即可得证;
(3)阴影部分的面积=三角形BOD的面积-扇形DOF的面积,求出即可.
解答: 解:(1)∵AB与圆O相切,
解:(1)∵AB与圆O相切,
∴OD⊥AB,
在Rt△BDO中,∠B=60°,BD=
,
∴tanB=
,
∴OD=BD•tan60°=3;
(2)连接OE,
∵AE=OD=3,AE∥OD,
∴四边形AEOD为平行四边形,
∴AD∥EO,
∵DA⊥AE,
∴OE⊥AC,
又∵OE为圆的半径,
∴AE为圆O的切线;
(3)在Rt△BDO中,BD=
,OD=3,
∴S△OBD=
BD•OD=
×
×3=
,
∵∠B=60°,
∴∠FOD=30°,
∴S扇形=
=
π,
∴S阴影=S△OBD-S扇形FOD=
-
π=
.
 解:(1)∵AB与圆O相切,
解:(1)∵AB与圆O相切,∴OD⊥AB,
在Rt△BDO中,∠B=60°,BD=
| 3 |
∴tanB=
| OD |
| BD |
∴OD=BD•tan60°=3;
(2)连接OE,
∵AE=OD=3,AE∥OD,
∴四边形AEOD为平行四边形,
∴AD∥EO,
∵DA⊥AE,
∴OE⊥AC,
又∵OE为圆的半径,
∴AE为圆O的切线;
(3)在Rt△BDO中,BD=
| 3 |
∴S△OBD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
∵∠B=60°,
∴∠FOD=30°,
∴S扇形=
| 30π×32 |
| 360 |
| 3 |
| 4 |
∴S阴影=S△OBD-S扇形FOD=
3
| ||
| 2 |
| 3 |
| 4 |
6
| ||
| 4 |
点评:此题考查了切线的判定与性质,扇形的面积,锐角三角函数定义,平行四边形的判定与性质,以及平行线的性质,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
两圆的半径R,r分别是方程x2-5x+6=0的两根,两圆圆心距为5,则两圆位置关系是( )
| A、外离 | B、内含 | C、相交 | D、相切 |
已知非零向量
、
、
,下列命题中是假命题的是( )
| a |
| b |
| c |
A、如果
| ||||||||||||
B、如果
| ||||||||||||
C、如果|
| ||||||||||||
D、如果
|
下列几组数:①9,12,15;②15,36,39;③12,35,35;④12,18,22.其中能组成直角三角形边长的是( )
| A、①和② | B、②和③ |
| C、③和④ | D、①和④ |
如果|
|=3.|
|=2,且
与
反向,那么下列关系中成立的是( )
| a |
| b |
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如果三角形的三个内角的比是3:4:7,那么这个三角形是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角三角形或钝角三角形 |
 如图,点P在线段AB上,点M、N分别是线段AB、AP的中点,若AB=16cm,BP=6cm,求线段NP和线段MN的长.
如图,点P在线段AB上,点M、N分别是线段AB、AP的中点,若AB=16cm,BP=6cm,求线段NP和线段MN的长.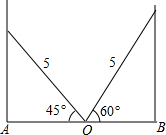 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45°,如果梯子的底端O固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60°,求此保管室的宽度AB的长.
如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45°,如果梯子的底端O固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60°,求此保管室的宽度AB的长.