题目内容
1.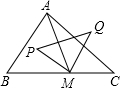 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
分析 根据三角形的外心的概念确定PQ是线段AM的垂直平分线,根据题意得到当AM⊥BC时,S△PMQ最小,计算即可.
解答 解:∵P、Q分别是△ABM、△ACM外接圆的圆心,
∴PQ是线段AM的垂直平分线,
∴S△PMQ=$\frac{1}{2}$×PQ×MH,
∴当AM⊥BC时,S△PMQ最小,
∵∠B=60°,∠C=45°,
∴AM=$\sqrt{3}$BM,AM=MC,
∴$\frac{\sqrt{3}}{3}$AM+AM=4+4$\sqrt{3}$,
解得,AM=4$\sqrt{3}$,
∵P、Q分别是△ABM、△ACM外接圆的圆心,
∴PQ=$\frac{1}{2}$BC=2+2$\sqrt{3}$,
∴S△PMQ=$\frac{1}{2}$×PQ×MH=6$\sqrt{3}$+12,
故答案为:6$\sqrt{3}$+12.
点评 本题考查的是三角形的外接圆和外心的概念和性质,掌握线段垂直平分线的判定定理、三角形中位线的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.若直线y=kx+b是由直线y=2x+4沿x轴向右平移4个单位所得,则k,b的值分别是( )
| A. | k=-2,b=-4 | B. | k=2,b=-4 | C. | k=-4,b=2 | D. | k=4,b=2 |
6.己知二次函数y=ax2+bx+c(a>0),对任意实数t,其图象都经过点(2+t,m)和点(2-t,m),又图象经过点(-1,y1),(2,y2),(6,y3),则函数值y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y3>y1>y2 | C. | y2>y1>y3 | D. | y3>y2>y1 |
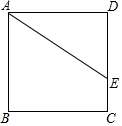 已知正方形ABCD中,点E在边DC上,DE=3,EC=1,如图所示,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为1或7.
已知正方形ABCD中,点E在边DC上,DE=3,EC=1,如图所示,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为1或7.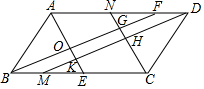 如图,在平行四边形ABCD中,AE,BF,CN,DM分别是∠DAB,∠ABC,∠BCD,∠CDA的角平分线,且相交于点O,K,H,G,求证:四边形HGOK是矩形.
如图,在平行四边形ABCD中,AE,BF,CN,DM分别是∠DAB,∠ABC,∠BCD,∠CDA的角平分线,且相交于点O,K,H,G,求证:四边形HGOK是矩形. 如图,已知D是△ABC内一点.
如图,已知D是△ABC内一点. 如图,在正方形ABCD中,F是对角线AC上任一点,BF⊥EF,AD=1.
如图,在正方形ABCD中,F是对角线AC上任一点,BF⊥EF,AD=1.