题目内容
9.用因式分解法解下列一元二次方程(1)x2=2x
(2)(x+1)2-(2x-3)2=0
(3)x2-6x+8=0
(4)4(x+3)2=25(x-2)2
(5)(1+$\sqrt{2}$)x2-(1-$\sqrt{2}$)x=0
(6)(2-3x)+(3x-2)2=0.
分析 (1)提公因式分解因式法求解可得;
(2)平方差公式分解因式求解可得;
(3)十字相乘法因式分解求解可得;
(4)平方差公式因式分解求解可得;
(5)提公因式法因式分解求解可得;
(6)提公因式法因式分解求解可得.
解答 解:(1)∵x2-2x=0,
∴x(x-2)=0,
则x=0或x-2=0,
解得:x=0或x=2;
(2)∵(x+1)2=(2x-3)2,
∴x+1=2x-3或x+1=3-2x,
解得:x=4或x=$\frac{2}{3}$;
(3)∵(x-2)(x-4)=0,
∴x-2=0或x-4=0,
解得:x=2或x=4;
(4)∵4(x+3)2-25(x-2)2=0,
∴(7x-4)(-3x+16)=0,
则7x-4=0或-3x+16=0,
解得:x=$\frac{4}{7}$或x=$\frac{16}{3}$;
(5)∵x[(1+$\sqrt{2}$)x-(1-$\sqrt{2}$)]=0,
则x=0或(1+$\sqrt{2}$)x-(1-$\sqrt{2}$)=0,
解得:x=0或x=-3+2$\sqrt{2}$;
(6)∵(2-3x)(1+2-3x)=0,
∴2-3x=0或3-3x=0,
解得:x=$\frac{2}{3}$或x=1.
点评 本题主要考查因式分解法解一元二次方程,熟练掌握因式分解的方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.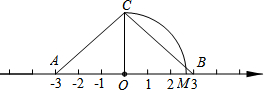 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )
如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )
 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )
如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )| A. | $\sqrt{7}$ | B. | 4 | C. | 5 | D. | 2.5 |
14. 将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表
将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表
则an=( )(用含n的代数式表示)
 将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表
将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表| 所剪次数 | 1 | 2 | 3 | 4 | … | n |
| 正三角形个数 | 4 | 7 | 10 | 13 | … | an |
| A. | 2n | B. | 3(n-1) | C. | 3(n+1) | D. | 3n+1 |
1.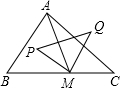 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12. 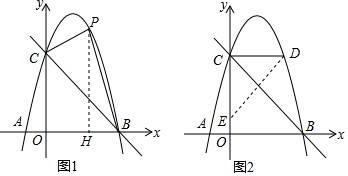
 如图,一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至的C10,(1)请写出抛物线C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段抛物线C10上,则m=-260.
如图,一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至的C10,(1)请写出抛物线C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段抛物线C10上,则m=-260. 如图,已知矩形ABCD中,FA、HB、FD、HC分别平分∠BAD、∠ABC、∠ADC、∠BCD.求证:四边形EFGH是正方形.
如图,已知矩形ABCD中,FA、HB、FD、HC分别平分∠BAD、∠ABC、∠ADC、∠BCD.求证:四边形EFGH是正方形.