题目内容
11. 如图,在正方形ABCD中,F是对角线AC上任一点,BF⊥EF,AD=1.
如图,在正方形ABCD中,F是对角线AC上任一点,BF⊥EF,AD=1.(1)求证:BF=EF;
(2)过点E作EG⊥AC,垂足为G,请问GF的长度是一个定值吗?如果是请求出这个长度的值,若不是请说明理由.
分析 (1)如图1中,作FM⊥AD于M,FN⊥AB于N.只要证明△FME≌△FNB即可.
(2)如图2中,GF的长度是一个定值.连接BD交AC于O.首先求出OB的长,再证明△EGF≌△FOB,即可推出FG=OB=$\frac{\sqrt{2}}{2}$.
解答 (1)证明:如图1中,作FM⊥AD于M,FN⊥AB于N.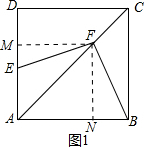
∵四边形ABCD是正方形,
∴∠CAD=∠CAB=45°,
∴FN=FM,
∵∠FMA=∠MAN=∠FNA=90°,
∴∠MFN=∠EFB=90°,
∴∠MFE=∠NFB,
在△FME和△FNB中,
$\left\{\begin{array}{l}{∠FME=∠FNB}\\{FM=FN}\\{∠MEE=∠NFB}\end{array}\right.$,
∴△FME≌△FNB,
∴EF=FB.
(2)如图2中,GF的长度是一个定值.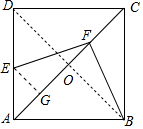
理由:连接BD交AC于O.
∵四边形ABCD是正方形,
∴AD=AB=BC=CD=1,BD=$\sqrt{2}$,OB=OD=$\frac{\sqrt{2}}{2}$,AC⊥BD,
∴∠EFB=∠BOF=∠EGF=90°,
∵∠EFG+∠FEG=90°,∠EFG+∠BFO=90°,
∴∠FEO=∠BFO,
在△EGF和△FOB中,
$\left\{\begin{array}{l}{∠EGF=∠FOB}\\{∠FEG=∠BFO}\\{EF=FB}\end{array}\right.$,
∴△EGF≌△FOB,
∴FG=OB=$\frac{\sqrt{2}}{2}$,
∴FG的长度是定值.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.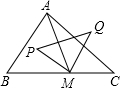 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
2.如果m表示有理数,那么|m|-m的值( )
| A. | 不可能是负数 | B. | 可能是零或者负数 | ||
| C. | 必定是零 | D. | 必定是正数 |
16.半径为1的圆的外切直角三角形的面积的最小值为( )
| A. | 3-$2\sqrt{2}$ | B. | 3+$2\sqrt{2}$ | C. | 6-4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
 如图,已知矩形ABCD中,FA、HB、FD、HC分别平分∠BAD、∠ABC、∠ADC、∠BCD.求证:四边形EFGH是正方形.
如图,已知矩形ABCD中,FA、HB、FD、HC分别平分∠BAD、∠ABC、∠ADC、∠BCD.求证:四边形EFGH是正方形.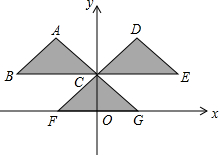 如图,三角形CFG的顶点坐标分别为C(0,$\frac{\sqrt{2}}{2}$),F(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移两次,构成如图所示的图案(其中点B、C、E在一条平行于x轴的直线上).
如图,三角形CFG的顶点坐标分别为C(0,$\frac{\sqrt{2}}{2}$),F(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移两次,构成如图所示的图案(其中点B、C、E在一条平行于x轴的直线上).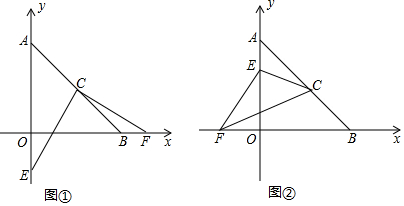
 如图,在△ABC中,AB=8,AC=6,点D在AC上,AD=2,若点E在AB上,以A,D,E为顶点的三角形与△ABC相似.求AE的长.
如图,在△ABC中,AB=8,AC=6,点D在AC上,AD=2,若点E在AB上,以A,D,E为顶点的三角形与△ABC相似.求AE的长.