题目内容
6.己知二次函数y=ax2+bx+c(a>0),对任意实数t,其图象都经过点(2+t,m)和点(2-t,m),又图象经过点(-1,y1),(2,y2),(6,y3),则函数值y1,y2,y3的大小关系是( )| A. | y1>y2>y3 | B. | y3>y1>y2 | C. | y2>y1>y3 | D. | y3>y2>y1 |
分析 由图象上的两点坐标求得抛物线对称轴,由开口方向知离对称轴水平距离越大的点,对应函数值越大,据此可得.
解答 解:∵图象都经过点(2+t,m)和点(2-t,m),
∴抛物线的对称轴为x=$\frac{2+t+2-t}{2}$=2,
又∵a>0,即抛物线的开口向上,
∴抛物线上离对称轴水平距离越大的点,对应函数值越大,
则y3>y1>y2,
故选:B.
点评 本题主要考查二次函数图象上点的坐标特征,根据题意得到抛物线的对称轴,结合开口方向知离对称轴水平距离越大的点,对应函数值越大是解题的关键.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
16.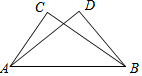 如图,已知∠ACB=∠ADB=90°,AC=BD.又因为公共边AB=BA,所以△ABC≌△BAD,其理由是( )
如图,已知∠ACB=∠ADB=90°,AC=BD.又因为公共边AB=BA,所以△ABC≌△BAD,其理由是( )
 如图,已知∠ACB=∠ADB=90°,AC=BD.又因为公共边AB=BA,所以△ABC≌△BAD,其理由是( )
如图,已知∠ACB=∠ADB=90°,AC=BD.又因为公共边AB=BA,所以△ABC≌△BAD,其理由是( )| A. | SAS | B. | ASA | C. | SSA | D. | HL |
14. 将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表
将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表
则an=( )(用含n的代数式表示)
 将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表
将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表| 所剪次数 | 1 | 2 | 3 | 4 | … | n |
| 正三角形个数 | 4 | 7 | 10 | 13 | … | an |
| A. | 2n | B. | 3(n-1) | C. | 3(n+1) | D. | 3n+1 |
1.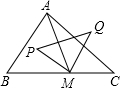 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
18.给出下列命题:①两边及一边上的中线对应相等的两个三角形全等;②底边和顶角对应相等的两个等腰三角形全等;③斜边和斜边上的高线对应相等的两个直角三角形全等,下列属于真命题的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
15.已知(-1,y1),(1,y2)是直线y=-9x+6上的两个点,则y1,y2的大小关系是( )
| A. | y1>0>y2 | B. | y1>y2>0 | C. | y2>0>y1 | D. | 0>y1>y2 |
16.半径为1的圆的外切直角三角形的面积的最小值为( )
| A. | 3-$2\sqrt{2}$ | B. | 3+$2\sqrt{2}$ | C. | 6-4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
 如图,在△ABC,AC的长为8cm,AC边上的高为BD,当B点在线段BD上向D点运动时,△ABC的面积发生了变化.
如图,在△ABC,AC的长为8cm,AC边上的高为BD,当B点在线段BD上向D点运动时,△ABC的面积发生了变化.